Добрый день всем! 

Сегодня я выкладываю видео, в котором пытаюсь понять сама и показать вам, как формируется любое поле - так сказать, поставим себя на место Творца. 

https://vk.com/geosiya?z=video53012486_456239248%2F752a13fe07b87c26fb%2Fpl_wall_53012486

Сегодня ч продолжаю публикацию видео  о силах притяжения. вашему вниманию представляю два видео. - первый показывает ,что все-таки нас прижимает к Земле, https://vk.com/video53012486_456239243

а во втором рассказываю, что позволяет нам двигаться

https://vk.com/video53012486_456239246

Добрый день!

Я обещала вам рассказать  кое о чем. Предлагаю посмотреть видео, в котором я рассказываю о Законе  Всемирного тяготения.

https://vk.com/video53012486_456239242

Добрый день, мои друзья!

   Занялся я тут историей астрономии, долго изучал Коперника и Птолемея и научился-таки считать по Птолемею - по таблицам и по аналитике, которую написал сам. А что такого - эпицикл на дифференте - простая кинематика.

   Вопрос - как из ЖЖ перенести текст с формулами сюда? И с кем бы мне обсудить результаты расчетов и их перспективы?)

 Все мы представляем Землю, насаженную на земную ось , этакую оглоблю, которая выписывает восьмерки и круги по небу. Однако в действительности никакой палки нет. Ось - это две точки на поверхности Земли. Внимание вопрос. Допустим сегодня на северном полюсе стоит гора Меру, а  сетка меридианов и параллелей привязана к мгновенному полюсу вращения. Как отразится прецессия Земли на координатах Меру?

Рассмотрим инерциальную систему отсчета XYZ и подвижную систему отсчета NKz. Последняя подвижна не только относительно инерциальной системы отсчета, но и относительно Земли.

Рис. 1.

Запишем теорему об изменении момента количества движения для подвижной системы отсчета NKz:

$\mathbf{\dot L}+\mathbf{\Omega} \times\mathbf{L}=\mathbf {M}$

где $\mathbf{L}$ - кинетический момент Земли,

$\mathbf{\Omega}$ - абсолютная угловая скорость системы координат NKz

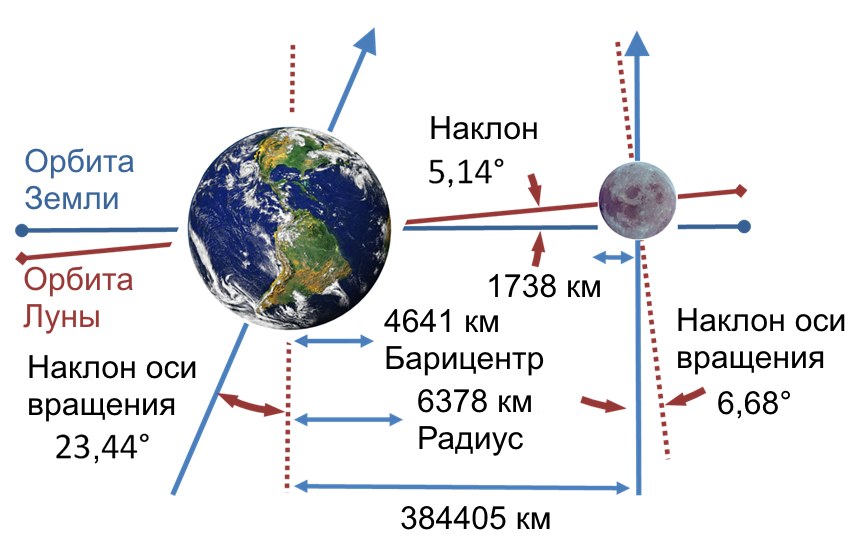
        Наконец-то я разобрался с влиянием приливов на наклон земной оси. 

Приливы уменьшают наклон земной оси к эклиптической нормали. Все просто! Приливы от Луны и Солнца стремятся поставить ось вращения Земли перпендикулярно плоскости эклиптики. Не я один пришел к такому выводу. Есть работы (Белецкий Владимир Васильевич), доказывающие это предположение.
Я получил количественные соотношения. Убывание наклона Земли к плоскости эклиптики.

Москва. 2 декабря. INTERFAX.RU - Посадочный модуль китайской автоматической станции "Чанъэ-5" в среду, успешно пробурив грунт Луны на глубину два метра, поднял образцы геологической породы и запаковал их в контейнер для предстоящей отправки на Землю, сообщило Национальное космическое управление Китая (CNSA).

Прошу специалистов помочь мне разобраться в вопросе или найти ошибку.