Траектория Луны в гелиоцентрической системе отсчета.

This research has made use of NASA's Astrophysics Data System
Луна в своем движении вокруг Солнца совершает довольно сложные маневры, пересекая орбиту Земли. Можно подумать, что ее траектория напоминает синусоиду, наложенную на эллипс. Но тогда местами кривизна траектории становится положительной, т.е. выпуклой в сторону Солнца, что существенно нарушает баланс сил инерции и гравитации.
Решение этого непростого вопроса я нашел в статье столетней давности
- 193 комментария
- Читать далее
- 37093 просмотра
Кинематические модели Птолемея

Занялся я тут историей астрономии, долго изучал Коперника и Птолемея и научился-таки считать по Птолемею - по таблицам и по аналитике, которую написал сам. А что такого - эпицикл на дифференте - простая кинематика.
Вопрос - как из ЖЖ перенести текст с формулами сюда? И с кем бы мне обсудить результаты расчетов и их перспективы?)
- Войдите на сайт для отправки комментариев
- Читать далее
- 6247 просмотров
Прецессия Земли и координаты полюса
Все мы представляем Землю, насаженную на земную ось ![]() , этакую оглоблю, которая выписывает восьмерки и круги по небу. Однако в действительности никакой палки нет. Ось - это две точки на поверхности Земли. Внимание вопрос. Допустим сегодня на северном полюсе стоит гора Меру, а сетка меридианов и параллелей привязана к мгновенному полюсу вращения. Как отразится прецессия Земли на координатах Меру?
, этакую оглоблю, которая выписывает восьмерки и круги по небу. Однако в действительности никакой палки нет. Ось - это две точки на поверхности Земли. Внимание вопрос. Допустим сегодня на северном полюсе стоит гора Меру, а сетка меридианов и параллелей привязана к мгновенному полюсу вращения. Как отразится прецессия Земли на координатах Меру?
- Войдите на сайт для отправки комментариев
- Читать далее
- 4284 просмотра
Приливы уменьшают наклон земной оси к эклиптической нормали
Рассмотрим инерциальную систему отсчета XYZ и подвижную систему отсчета NKz. Последняя подвижна не только относительно инерциальной системы отсчета, но и относительно Земли.
.jpg) Рис. 1.
Рис. 1.
Запишем теорему об изменении момента количества движения для подвижной системы отсчета NKz:
$\mathbf{\dot L}+\mathbf{\Omega} \times\mathbf{L}=\mathbf {M}$
где $\mathbf{L}$ - кинетический момент Земли,
$\mathbf{\Omega}$ - абсолютная угловая скорость системы координат NKz
- Войдите на сайт для отправки комментариев
- Читать далее
- 5333 просмотра
Луна и наклон земной оси
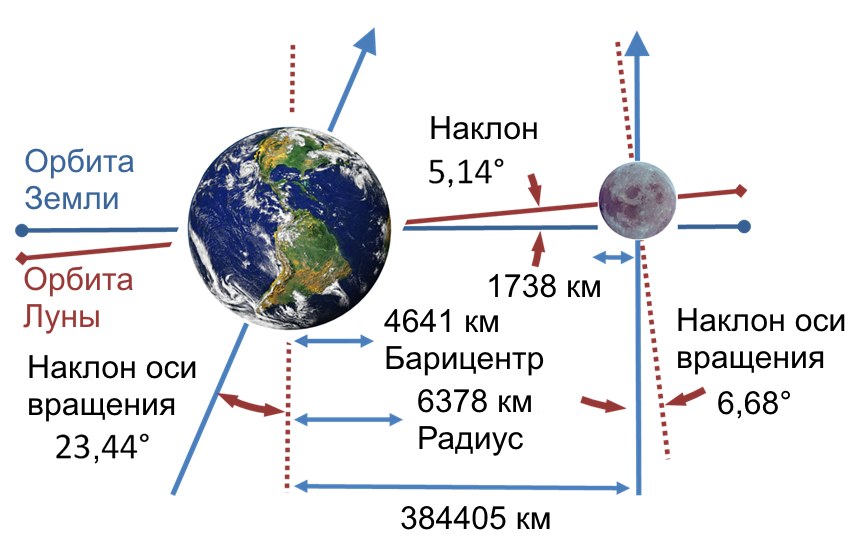
Наконец-то я разобрался с влиянием приливов на наклон земной оси.
Приливы уменьшают наклон земной оси к эклиптической нормали. Все просто! Приливы от Луны и Солнца стремятся поставить ось вращения Земли перпендикулярно плоскости эклиптики. Не я один пришел к такому выводу. Есть работы (Белецкий Владимир Васильевич), доказывающие это предположение.
Я получил количественные соотношения. Убывание наклона Земли к плоскости эклиптики.
- 1 комментарий
- Читать далее
- 6955 просмотров
Китайцы бурят Луну
Москва. 2 декабря. INTERFAX.RU - Посадочный модуль китайской автоматической станции "Чанъэ-5" в среду, успешно пробурив грунт Луны на глубину два метра, поднял образцы геологической породы и запаковал их в контейнер для предстоящей отправки на Землю, сообщило Национальное космическое управление Китая (CNSA).
- Войдите на сайт для отправки комментариев
- 3418 просмотров
Приливы и наклон земной оси
Прошу специалистов помочь мне разобраться в вопросе или найти ошибку.

- 18 комментариев
- Читать далее
- 5694 просмотра
Изменение звездных суток в прошлом и будущем
Из закона сохранения момента импульса системы Земля Луна (без учета наклона оси вращения Земли)
$L=С\omega + \mu x^2 \Omega = const$
где $C$ - полярный момент инерции Земли, $\omega$ - угловая скорость вращения Земли, соответствующая звездным суткам, $\Omega$ - угловая скорость вращения системы Земля-Луна вокруг барицентра, $\mu$ - приведенная масса системы, $x$ - расстояние между центрами Земли и Луны
следует, что угловая скорость собственного вращения Земли зависит от расстояния между центрами Земли и Луны так:
- 10 комментариев
- Читать далее
- 5775 просмотров
Приливная эволюция системы Земля-Луна
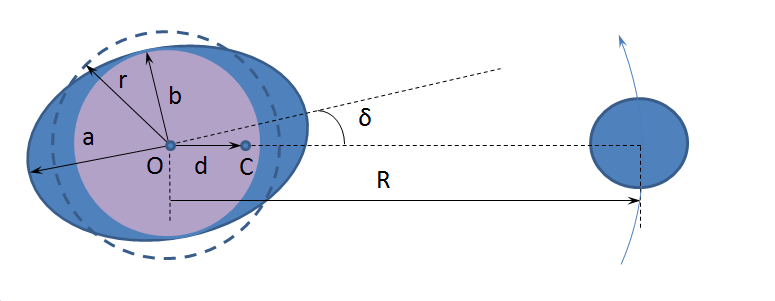
Рис. 1.
- Войдите на сайт для отправки комментариев
- Читать далее
- 6224 просмотра
Приливы увеличивают наклон земной оси к плоскости эклиптики
В ДАННОЙ РАБОТЕ СОДЕРЖИТСЯ ОШИБКА, ПРИВОДЯЩАЯ К ОБРАТНОМУ РЕЗУЛЬТАТУ. МЕТОДОЛОГИЧЕСКИ ВСЕ ВЕРНО, НО ГДЕ-ТО ПОТЕРЯН ЗНАК.
В ИТОГЕ, ПРАВИЛЬНО СЧИТАТЬ, ЧТО ПРИЛИВЫ УВЕЛИЧИВАЮТ НАКЛОН ЗЕМНОЙ ОСИ К ПЛОСКОСТИ ЭКЛИПТИКИ (А НЕ К НОРМАЛИ)
Рассмотрим систему координат ONKz, подвижную, как в Земле, так и в инерциальном пространстве. Уравнения движения Земли под действием момента сил со стороны Луны в этой системе можно найти в работе [1].
- 3 комментария
- Читать далее
- 7685 просмотров
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- следующая ›
- последняя »


