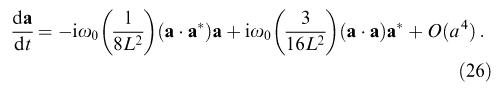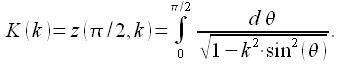Прецессия сферического маятника
Опубликовано Ingus в вс, 13/05/2012 - 10:46
in
Данный материал выставлен в личном блоге без предварительного рецензирования.
Уравнения движения сферического маятника впервые были получены еще в 18 веке. Кривая, которую выписывает сферический маятник, изучена Клеро в 1735 году, Лагранжем и Пюизе в 1842 году.
Виктор Пюизе показал, что если маятник совершает эллиптическое движение, возникает эффект самопрецессии эллипса, пропорциональный его площади и обратно пропорциональный квадрату длины маятника:
(1)
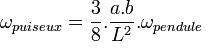
Эта же формула приводится в работе Б.Я. Зельдовича и М. Дж. Суало как результат решения векторного уравнения для эллиптически поляризованного движения маятника[1].
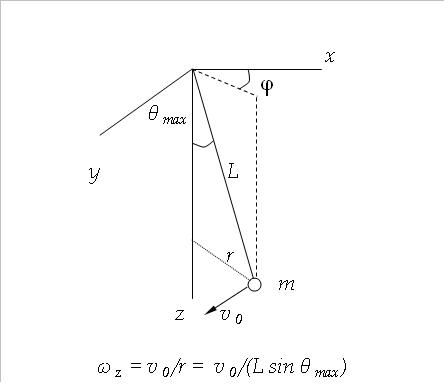
Если начальный угол отклонения маятника от вертикали известен (большая полуось эллипса), то малую полуось нужно еще найти. Поэтому перепишем формулу (1) в других обозначениях, через осевую частоту ωz (Рис. 1.).
Рис.1. Параметры движения сферического маятника.
Параметры эллипса можно оценить, только предполагая колебания маятника малыми[2]
Откуда
а=х0= L sin(θmax), b=v0/ω0= ωz L sin(θmax)/ ω0,
поскольку v0=ωz L sin(θmax)
В новой записи частота прецессии будет выглядеть следующим образом (3/8=0,375):
ωp=0,375 ωz sin2(θmax) (2)
Проверить точность данной формулы можно, осуществив численное моделирование процесса для различных режимов движения маятника, варьируя параметры ωz и θmax.
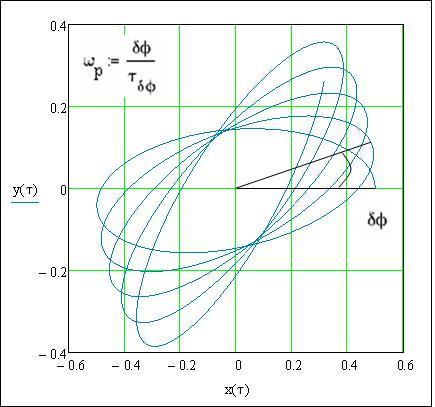
Рис.2. Проекция траектории маятника на плоскость ХОY (θmax=π/6, ωz/ω0 =0,3)
Частоту прецессии естественным образом можно вычислить по смещению лепестка «ромашки» (Рис.2.):
ωp= δφ/τδφ
т.е. частота прецессии равна отношению угла поворота лепестка и времени этого поворота.
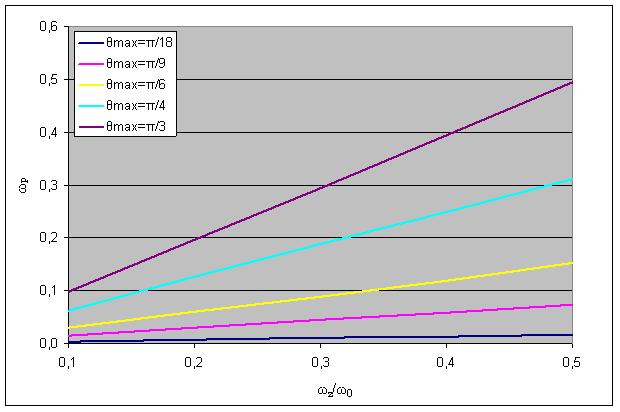
Рис. 3. Зависимость частоты самопрецессии от отношения осевой и собственной частот для различных углов отклонения маятника.
Как видно из Рис. 3, угол наклона прямых для различных значений θmax возрастает нелинейно. Однако есть способ линеаризовать эту зависимость (Рис. 4).
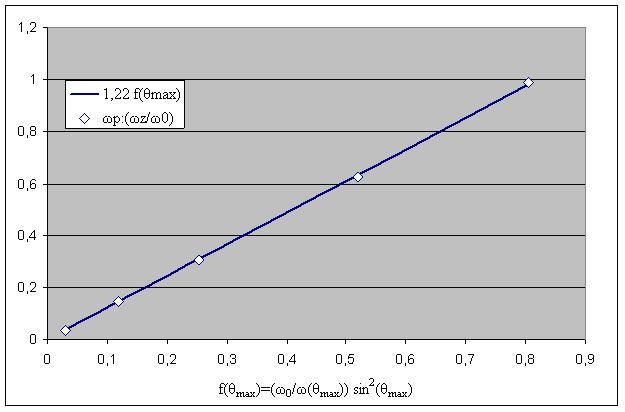
Рис. 4. Линеаризация зависимости частоты самопрецессии от сложного параметра f(θmax).
В результате численного моделирования мы получили формулу для частоты самопрецессии эллипса в виде:
ωp=1,22 (ω0/ω(θmax)) sin2(θmax)( ωz/ω0) (3)
Отношение ω0/ω(θmax) следует раскрыть через полный эллиптический интеграл
2K(k)/ π = ω0/ ω(k)= ω0/ω(θmax), где k=sin(θmax/2)
В итоге получим
ωp=1,22 (2K(k)/ π) (ωz/ω0) sin2(θmax) (4)
и сравним с (2), несколько видоизменив последнюю, для удобства сравнения:
ωp=3/8 ω0 (ωz/ω0) sin2(θmax) (5)
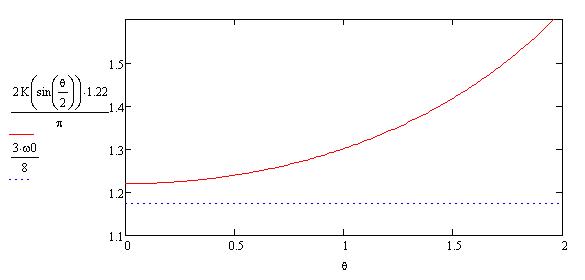
Осталось понять, как относятся 1,22 (2K(k)/ π) и 3/8 ω0
Рис. 5. Сравнение коэффициентов для расчета частоты самопрецессии.
Итак, в результате численного моделирования движения сферического маятника без каких бы то ни было ограничений на малость колебаний получена формула для расчета частоты самопрецессии траектории маятника и показано, что оценка этой частоты В.Пюизе была занижена, по-видимому по причине допущения о малости колебаний.
Формула Пюизе гораздо лучше работает для малых углов отклонения, если заменить в ней 3 на π, памятуя, что площадь эллипса равна Sэ=π a b.
Тогда ωp= Sэ ω0/8L2 (6)
Вернемся теперь к формуле (3) и выразим частоту прецессии через осевые моменты импульса,
переписав ее в следующем виде:
ωp=1,22 (ωz/ω(θmax)) sin2(θmax) (7)
Момент импульса сферического маятника относительно вертикальной оси z равен
Mz= mL2 sin2(θmax) ωz=const. (8)
Момент импульса плоского математического маятника в нелинейном приближении равен
Mx=mL2ω(θmax) (9)
Откуда:
ωp=1,22 Mz /Mx (10)
Осталось только выразить коэффициент 1,22 через параметры маятника.
[1] Б.Я. Зельдович, М.Дж. Суало «Двухчастотный маятник на вращающейся платформе: моделирование оптических явлений»
[2] Бухгольц Н.Н. Основной курс теоретической механики (том 1) Кинематика, статика, динамика материальной точки. 1965
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 9329 просмотров
