Данный материал выставлен в личном блоге без предварительного рецензирования.
С давних времен принято считать орбиту Луны кеплеровским эллипсом с хорошо известными большой полуосью и эксцентриситетом. Однако, если мы рассмотрим движение Луны в гелиоцентрической системе отсчета , то увидим такую картину:
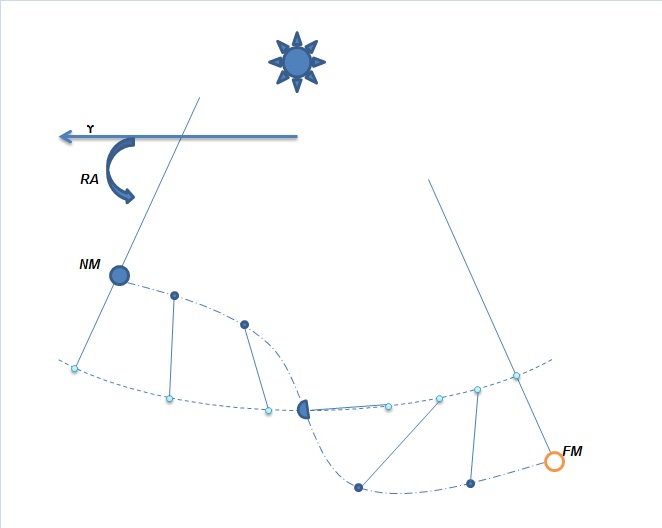
Рис. 1. Путь Луны относительно Земли в гелиоцентрической системе отсчета.
Пара Земля-Луна совершает замысловатый танец с обгонами и отставаниями таким образом, что кажется будто Луна вращается вокруг Земли. В геоцентрической системе орбита Луны действительно напоминает эллипс с перигеем и апогеем. Однако, если мы внимательно посмотрим эфемериды, то обнаружим, что апогей никогда не бывает напротив перигея.
| DMY | RА | D | R | APS | RAp+12-RAa |
| 05.01.2000 | 17,64 | -20,0 | 406346 | A | |
| 20.01.2000 | 6,89 | 20,9 | 359399 | P | |
| 01.02.2000 | 17,40 | -19,6 | 405605 | A | 1,490 |
| 17.02.2000 | 7,53 | 20,6 | 364549 | P | |
| 29.02.2000 | 17,97 | -20,6 | 404595 | A | 1,553 |
| 15.03.2000 | 7,23 | 21,0 | 369593 | P | |
| 28.03.2000 | 18,53 | -21,2 | 404106 | A | 0,696 |
| 09.04.2000 | 4,98 | 19,1 | 368317 | P | |
| 25.04.2000 | 19,10 | -21,4 | 404410 | A | -2,121 |
| 06.05.2000 | 4,65 | 18,4 | 363313 | P | |
| 22.05.2000 | 18,85 | -21,7 | 405418 | A | -2,195 |
| 04.06.2000 | 6,34 | 21,5 | 359305 | P | |
| 19.06.2000 | 19,47 | -21,5 | 406048 | A | -1,132 |
| 02.07.2000 | 6,95 | 21,7 | 357395 | P | |
| 16.07.2000 | 19,26 | -21,6 | 406191 | A | -0,308 |
| 30.07.2000 | 7,55 | 21,4 | 358488 | P | |
| 12.08.2000 | 19,03 | -21,7 | 405702 | A | 0,518 |
| 28.08.2000 | 9,22 | 18,1 | 362055 | P | |
| 09.09.2000 | 19,64 | -21,5 | 404697 | A | 1,585 |
| 24.09.2000 | 8,87 | 19,2 | 367018 | P | |
| 06.10.2000 | 19,36 | -21,9 | 404184 | A | 1,508 |
| 20.10.2000 | 7,63 | 21,8 | 370107 | P | |
| 03.11.2000 | 19,93 | -21,6 | 404431 | A | -0,302 |
Далее, если мы построим по точкам орбиту Луны в декартовых координатах, зная ее прямое восхождение RA и геоцентрическое расстояние, то получим кривую не отличимую на глаз от окружности, что и понятно, так как официально эксцентриситет орбиты Луны составляет 0,055.
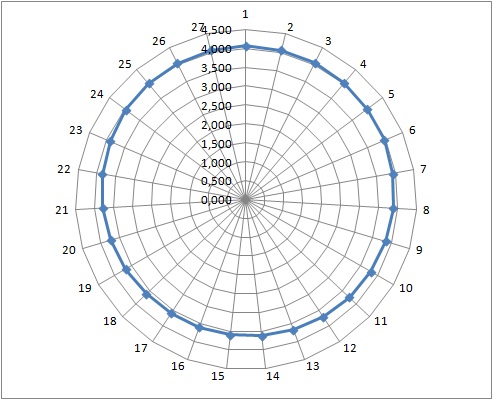
Рис. 2 Орбита Луны в декартовых координатах.
Но насколько эллипс отличается от окружности? По всей видимости лучшей аппроксимацией эллипса с полуосями а и b будет концентрическая окружность радиуса (a+b)/2. Максимальное расхождение этих кривых для Луны составляет около 300 км.
Попробуем найти центр кривой, изображенной на Рис. 2. Для этого воспользуемся триангуляционным методом, который кстати намного эффективнее МНК - метода наименьших квадратов. Суть метода такова. Берем все возможные тройки точек отстоящие друг от друга примерно на 4 часа, если пользоваться аналогией с циферблатом. Находим по известным формулам http://en.wikipedia.org/wiki/Circumscribed_circle центры описанных около этих точек окружностей.
.jpg)
Затем осредняем координаты центров и находим окружность менее всего уклоняющуюся от исследуемой нами кривой. Результаты расчетов отражены в следующей таблице. Исследуемые точки орбиты ложатся на окружность радиуса 383800 км, причем максмальное отклонение от нее не превышает 3000 км, т.е. меньше радиуса Земли. Центр окружности находится на расстоянии 23500 км от центра Земли.
| DMY | Ra | x' | y' | ||||||
| 01.01.2000 | 14,45 | -3,216 | -2,395 | ||||||
| 02.01.2000 | 15,22 | -2,687 | -3,013 | X0 | Y0 | ||||
| 03.01.2000 | 16,01 | -2,022 | -3,515 | 0,034 | -0,233 | ||||
| 04.01.2000 | 16,81 | -1,243 | -3,868 | Xc | Yc | R | d,км | ||
| 05.01.2000 | 17,64 | -0,385 | -4,045 | A | 74,879 | 0,047 | -0,236 | 3,835 | -286 |
| 06.01.2000 | 18,48 | 0,508 | -4,025 | 74,579 | 0,049 | -0,221 | 3,821 | -1682 | |
| 07.01.2000 | 19,33 | 1,380 | -3,801 | 74,341 | 0,041 | -0,212 | 3,813 | -2473 | |
| 08.01.2000 | 20,18 | 2,175 | -3,387 | 74,278 | 0,028 | -0,211 | 3,812 | -2609 | |
| 09.01.2000 | 21,02 | 2,847 | -2,812 | 74,434 | 0,017 | -0,219 | 3,816 | -2186 | |
| 10.01.2000 | 21,85 | 3,362 | -2,116 | 74,772 | 0,013 | -0,232 | 3,824 | -1406 | |
| 11.01.2000 | 22,67 | 3,703 | -1,341 | 75,172 | 0,016 | -0,245 | 3,833 | -510 | |
| 12.01.2000 | 23,48 | 3,864 | -0,526 | 75,483 | 0,026 | -0,254 | 3,841 | 285 | |
| 13.01.2000 | 0,29 | 3,844 | 0,296 | B | 75,613 | 0,038 | -0,254 | 3,846 | 831 |
| 14.01.2000 | 1,12 | 3,646 | 1,096 | 75,580 | 0,047 | -0,245 | 3,849 | 1067 | |
| 15.01.2000 | 1,96 | 3,272 | 1,846 | 75,483 | 0,048 | -0,232 | 3,848 | 1015 | |
| 16.01.2000 | 2,85 | 2,723 | 2,516 | 75,408 | 0,039 | -0,218 | 3,846 | 759 | |
| 17.01.2000 | 3,79 | 2,006 | 3,064 | 75,373 | 0,023 | -0,211 | 3,842 | 394 | |
| 18.01.2000 | 4,78 | 1,139 | 3,442 | 75,319 | 0,007 | -0,215 | 3,838 | -17 | |
| 19.01.2000 | 5,82 | 0,168 | 3,598 | 75,146 | -0,003 | -0,227 | 3,833 | -464 | |
| 20.01.2000 | 6,89 | -0,833 | 3,496 | 74,782 | -0,003 | -0,243 | 3,829 | -942 | |
| 21.01.2000 | 7,97 | -1,773 | 3,137 | 74,245 | 0,008 | -0,256 | 3,824 | -1363 | |
| 22.01.2000 | 9,00 | -2,571 | 2,564 | C | 73,660 | 0,026 | -0,257 | 3,823 | -1548 |
| 23.01.2000 | 9,99 | -3,178 | 1,843 | 73,191 | 0,042 | -0,246 | 3,825 | -1318 | |
| 24.01.2000 | 10,92 | -3,581 | 1,039 | 72,960 | 0,050 | -0,224 | 3,832 | -621 | |
| 25.01.2000 | 11,80 | -3,783 | 0,202 | 73,004 | 0,045 | -0,200 | 3,842 | 419 | |
| 26.01.2000 | 12,63 | -3,799 | -0,629 | 73,293 | 0,031 | -0,181 | 3,853 | 1550 | |
| 27.01.2000 | 13,43 | -3,639 | -1,428 | 73,753 | 0,012 | -0,174 | 3,863 | 2479 | |
| 28.01.2000 | 14,21 | -3,315 | -2,168 | 74,292 | -0,003 | -0,179 | 3,868 | 2960 |
Совокупность промежуточных центров удивительным образом сама ложится на оружность Рис.3.
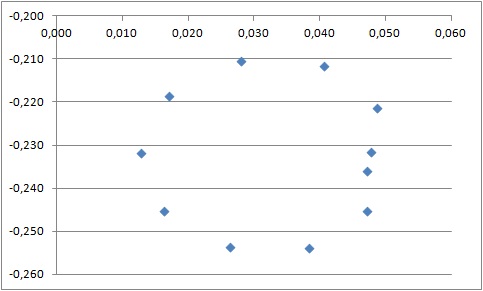
Рис. 3. Центры описанных около треугольников окружностей в методе аппроксимации точек окружностью.
Подобный расчет для различных месяцев года показал, что вычисленный таким образом радиус орбиты не меняется месяц от месяца в течении года, т.е. не зависит от расстояния между Землей и Солнцем, что в общем то удивительно лишь отчасти, поскольку период изменения перигей-апогейного расстояния имеет период в 206 сут, что не соизмеримо с полугодием.
Итак, орбита Луны в геоцентрической системе отсчета я вляется строгой окружностью неизменного во времени! радиуса 383800 км, центр которой отстоит от центра Земли на величину порядка 23000 км.
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 7394 просмотра


