Такой вывод можно сделать, проделав следующий простой расчет. Рассмотрим пару Земля – Луна в их обращении вокруг центра масс по строго круговым орбитам. Для решения задачи нам потребуется найти моменты сил, действующих на Землю со стороны Луны: главный момент, связанный с действием Луны на экваториальные вздутия Земли и вторичный момент, возникающий от действия Луны на приливные вздутия. Найдем главный момент (Рис.1.)
Рассмотрим две системы координат: Oxyz – система, связанная с главными центральными осями инерции Земли, и OXYZ – орбитальная система координат. Связь между этими системами осуществляется посредством матрицы поворота или матрицы направляющих косинусов $\boldsymbol{A}$.
.jpg)
Рис.1.
$\boldsymbol{A}=$$\begin{pmatrix} \cos\psi \cos\varphi - \sin\psi \cos\theta \sin\varphi & - \cos\psi \sin\varphi - \sin\psi\cos\theta \cos\varphi & \sin\psi \sin\theta \\sin\psi cos\varphi + \cos\psi \cos\theta \sin\varphi & \cos\psi \cos\theta \cos\varphi - \sin\psi \sin\varphi & - \cos\psi \sin\theta \\ \sin\theta \sin\varphi & \sin\theta \cos\varphi & \cos\theta \end{pmatrix}$ (1)
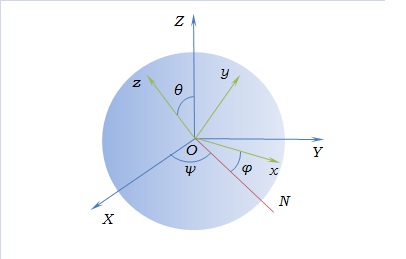
Рис. 2.
Направляющие косинусы связаны с углами Эйлера (Рис. 2.) следующими соотношениями:
$a_{11}=\cos\psi \cos\varphi - \sin\psi \cos\theta \sin\varphi\\a_{12}= - \cos\psi \sin\varphi - \sin\psi\cos\theta \cos\varphi\\a_{13} =\sin\psi \sin\theta \\a_{21}=\sin\psi cos\varphi + \cos\psi \cos\theta \sin\varphi\\a_{22} =\cos\psi \cos\theta \cos\varphi - \sin\psi \sin\varphi \\a_{23}= - \cos\psi \sin\theta \\a_{31}= \sin\theta \sin\varphi \\a_{32} =\sin\theta \cos\varphi \\a_{33}= \cos\theta$ (2)
Эта матрица позволяет по известным координатам вектора в системе Oxyz найти его координаты в системе OXYZ.
$\begin{pmatrix} X \\Y\\Z\end{pmatrix}=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\begin{pmatrix} x \\y\\z\end{pmatrix}$ (3)
Чтобы осуществить обратный переход, нужна матрица, обратная $\boldsymbol{A}$. К счастью, матрица поворота является ортогональной, т.е. чтобы найти обратную ей, достаточно ее транспонировать. Таким образом,
$\begin{pmatrix} x \\y\\z\end{pmatrix} =\begin{pmatrix} a_{11} & a_{21} & a_{31} \\a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{pmatrix} \begin{pmatrix} X \\Y\\Z\end{pmatrix} $ (4)
На элементарную массу dm в теле Земли со стороны Луны действует сила:
$d\boldsymbol{F}=-\frac{\mu}{\rho^3}\boldsymbol{\rho}dm $ (5)
где $\mu$ – гравитационный параметр Луны.
Момент, создаваемый этой силой относительно центра масс Земли равен:
$\boldsymbol{M}=\int \boldsymbol{r}\times d\boldsymbol{F} = -\mu \int \frac{\boldsymbol{r}\times \boldsymbol{\rho}}{\rho^3}dm $ (6)
Радиус вектор элементарной массы dm является суммой векторов $\boldsymbol{R}$ и $\boldsymbol{r}$,
$\boldsymbol{\rho}=\boldsymbol{R}+\boldsymbol{r}$ (7)
а его модуль равен:
$\rho=(R^2+r^2+2\boldsymbol{R}\cdot \boldsymbol{r})^{1/2}=R \left( 1+\frac{2\boldsymbol{R}\cdot \boldsymbol{r}}{R^2}+\frac{r^2}{R^2}\right)^{1/2}$ (8)
В случае с Луной величиной $\frac{r^2}{R^2}$ можно пожертвовать без существенной потери точности.
Следовательно,
$\frac{1}{\rho^3}=\frac{1}{R^3}\left(1-3\frac{\boldsymbol{R}\cdot \boldsymbol{r}}{R^2}\right)$ (9)
Вспомним, что векторное произведение вектора самого на себя равно нулю:
$\boldsymbol{r}\times\boldsymbol{\rho}=\boldsymbol{r}\times(\boldsymbol{R}+\boldsymbol{r})=\boldsymbol{r}\times\boldsymbol{R} $ (10)
Результирующий момент теперь можно представить как сумму двух интегралов:
$\boldsymbol{M_1}=-\mu\int \frac{\boldsymbol{r}\times\boldsymbol{R}}{R^3}dm $ (11)
$\boldsymbol{M_2}=\frac{3\mu}{R^5}\int (\boldsymbol{r}\times\boldsymbol{R})(\boldsymbol{r}\cdot \boldsymbol{R})dm$ (12)
Первый интеграл равен нулю, поскольку интегралы вида $\int xdm,\int ydm,\int zdm$ по объему тела (Земли) равны нулю.
В качестве упражнения можно доказать равенство:
$(\boldsymbol{r}\times\boldsymbol{R})(\boldsymbol{r}\cdot \boldsymbol{R})=\boldsymbol{R}\times(\boldsymbol{I}\cdot\boldsymbol{R}) $ (13)
где $\boldsymbol{I}$ - матрица вида
$I=\begin{bmatrix}y^2+z^2 &-xy &-xz \\ -xy&x^2+z^2 &-yz \\-xz &-yz &x^2+y^2\end{bmatrix}$ (14)
Тогда:
$\boldsymbol{M_2}=\frac{3\mu}{R^3}\frac{\boldsymbol{R}\times(\boldsymbol{J}\cdot \boldsymbol{R})}{R^2} $ (15)
где $\boldsymbol{J}$ - классическая матрица тензора инерции твердого тела.
Отношение вектора $\boldsymbol{R}$ к своему модулю есть единичный вектор, задающий его направление.
$\boldsymbol{\alpha}=\frac{\boldsymbol{R}}{R}=\begin{pmatrix}a_{11}\\ a_{12}\\ a_{13}\end{pmatrix} $ (16)
Следовательно,
$\boldsymbol{M_2}=\frac{3\mu}{R^3}{\boldsymbol{\alpha}\times(\boldsymbol{J}\cdot \boldsymbol{\alpha})}$ (17)
или, в проекции на оси орбитальной системы координат:
$\\ {M_x}=\frac{3\mu}{R^3}(C-B)a_{12}a_{13}\\{M_y}=\frac{3\mu}{R^3}(A-C)a_{11}a_{13}\\{M_z}=\frac{3\mu}{R^3}(B-A)a_{11}a_{12} $ (18)
где, А, В, С - главные центральные моменты инерции Земли.
Трансверсальную силу, действующую на приливные вздутия можно оценить как $2.204\cdot10^8$ Н (http://www.spacephys.ru/pochemu-udalyaetsya-luna-metodicheskaya-zarisovka). Момент, порождаемый приливными силами, обозначим $\boldsymbol{N}$. Механизм его возникновения таков: приливные горбы сносятся суточным вращением Земли, отчего возникает трансверсальная компонента равнодействующей силы притяжения. Эта компонента разгоняет Луну по орбите. Равная ей по величине и противоположная по направлению сила замедляет вращение Земли, создавая тормозящий момент. Величина тормозящего момента имеет порядок $10^{15}$ Н м.
Проекции этого момента на главные центральные оси инерции Земли есть:
$\\ {N_x}=N a_{31} \\{N_y}= N a_{32} \\{N_z}= N a_{33}$ (19)
Теперь можно записать динамические уравнения Эйлера:
$\\ A\dot{p}+(C-B)qr={M_x}-{N_x}\\B\dot{q}+(A-C)pr={M_y}-{N_y}\\C\dot{r}+(B-A)pq={M_z}-{N_z}$ (20)
где p,q,r – компоненты вектора угловой скорости вращения тела Земли около ее центра масс в базисе, связанном с главными центральными моментами инерции.
Угловая скорость вращения Земли есть сумма двух векторов – угловой скорости вращения тела Земли около центра масс Земли $\omega$ и угловой скорости вращения центра масс Земли около центра масс Земли и Луны $\Omega$.
Компоненты первого вектора:
$\\\omega_x=\dot{\psi}\sin\theta\sin\varphi+\dot{\theta}\cos\varphi\\\omega_y=\dot{\psi}\sin\theta\cos\varphi-\dot{\theta}\sin\varphi\\\omega_z=\dot{\psi}\cos\theta+\dot\varphi\\ $ (21)
Компоненты второго вектора:
$\\\Omega_x=\Omega a_{31}=\Omega\sin\theta\sin\varphi\\\Omega_y=\Omega a_{32}=\Omega\sin\theta\cos\varphi\\\Omega_z=\Omega a_{33}=\Omega\cos\theta\\ $ (22)
Компоненты вектора абсолютной угловой скорости равны:
$\\p=(\dot{\psi}+\Omega)\sin\theta\sin\varphi+\dot{\theta}\cos\varphi\\q=(\dot{\psi}+\Omega)\sin\theta\cos\varphi-\dot{\theta}\sin\varphi\\r=(\dot{\psi}+\Omega)\cos\theta+\dot\varphi\\$ (23)
Выведем отсюда производные эйлеровых углов:
$\\\dot{\psi}=(p\sin\varphi+q\cos\varphi)\csc\theta-\Omega\\\dot{\theta}=(p\cos\varphi-q\sin\varphi)\\\dot{\varphi}=r-(p\sin\varphi+q\cos\varphi)\cot\theta\\ $ (24)
Угловая скорость обращения Земли около барицентра системы Земля-Луна равна:
$\Omega=\sqrt\frac{\lambda+\mu}{R^3} $ (25)
где $\lambda$, $\mu$ гравитационные параметры Земли и Луны.
Итак, допустим, что Луна движется по круговой орбите, т.е. R=const, $\Omega$=const. Действие Луны на экваториальные вздутия Земли приводит к прецессии земной оси. К слову, в далеком прошлом, когда Луна была ближе, а Земля вращалась быстрее и от этого была более сжатой, постоянная прецессии очевидно была выше.
Действие Луны на приливные вздутия приводит к несколько иным последствиям. Вращение Земли замедляется. Энергия рассеивается приливным трением безвозвратно. Следовательно, изменение наклона земной оси может носить необратимый характер, как в случае волчка с трением: трение сначала "съедает" нутацию, а потом берется за наклон.
Можно попробовать завысить момент приливного взаимодействия до $10^{20}$, чтобы определить тенденцию его влияния на наклон Земной оси. Результат можно видеть на Рис. 3. В течение года наклон заметно увеличивается!
.jpg)
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 5913 просмотров



Уважаемый Иван!
Представленный вывод требует некоторых дополнений. В тексте не указано, что такое $A,B,C$. Я так думаю, что это главные осевые моменты инерции Земли, но надо это указать явно.
Второе необходимое дополнение - это сведения о моменте приливных сил ${\bf N}=(N_x,N_y,N_z)$. Формулы (19) и (20) необходимо дополнить сведениями о физическом происхождении этого момента и его математическом выражении. Без этого график повисает в воздухе.
Если излагать свою точку зрения, то следует это делать достаточно подробно для понимания Ваших выводов всеми. Более того, общие сведения о воздействии Луны на ось вращения Земли утверждают, что Луна как раз стабилизирует ось. Вполне возможно, что на Вашем графике только небольшая часть очень длинной огибающей в форме, близкой к синусоиде. Например, известно, что период прецессии земной оси порядка 26 000 лет. Для выяснения тенденции обычно используют теорию возмущений и качественный анализ системы уравнений. Вот есть такая полезная книжка: Н.Н. Баутин, Е.А. Леонтович. Методы и приемы качественного исследования динамических систем на плоскости. Серия ``Справочная математическая библиотека''. Вып. 11. М.: Наука, 1989. 489 с. Если надо, то перешлю по e-почте в электронном виде.
Уважаемый Виктор Михайлович!
Благодарю за ценные замечания!
Осевые моменты указал.
Вывод выражения для приливных сил содержится в моей предыдущей работе, на которую я и сослался http://www.spacephys.ru/pochemu-udalyaetsya-luna-metodicheskaya-zarisovka)">http://(http://www.spacephys.ru/pochemu-udalyaetsya-luna-metodicheskaya-zarisovka). Математическое вражение для момента существует:
$N=\frac{3\mu m R_e^3 \sin2\delta}{R^4}$
где $\mu$ - гравитационный параметр Луны, $m$ - масса приливного горба, $R_e$ - радиус Земли, $R$ - расстояние Земля-Луна, $\delta$ - угол сдвига приливного горба.
Проблема в том, что мы не знаем точно массу приливных горбов и их сдвиг. Однако трансверсальную силу мы можем оценить в численном эксперименте, зная скорость удаления Луны в настоящее время. Момент получается умножением этой силы на радиус Земли.
Я тоже утверждал в свое время, что Луна стабилизирует земную ось. Верю и сейчас. К сожалению этому нет доказательств. Если они Вам известны, буду очень признателен. С работами Ласкара знаком.
Книжку нашел. Изучаю.
Понятно, что линейное увеличение наклона земной оси может быть частью синусоиды гигантского периода, но... Замеделение вращения Земли необратимо. Фазовая траектория системы с трением не замкнута.