Георгий: Избранные вопросы расчёта траекторий космических тел с анализом механики движения.
Опубликовано Георгий в чт, 27/02/2020 - 11:53
Цель данного раздела состоит в формировании у читателя чёткого понятия о 4-ёх законах механики Ньютона для их правильного применения, например, в неинерциальных системах для расчёта космических траекторий с учётом дополнительных "фиктивных" сил инерции, появляющихся в этих системах. Будет поизведена попытка изложения основ расчёта космических тел с позиций классической механики с разбором избранных вопросов расчёта движения материального тела и доступным анализом действующих сил с учётом особенностей выбранной системы отсчёта (инерциальная, неинерциальная).
Георгий. 27.02.2020г. Время моск.
- Войдите на сайт для отправки комментариев
- 8464 просмотра



Уважаемый Георгий!
Вы не проверяли траекторию МКС в соответствии с анализом механики движения? Двигатели на МКС, конечно, подправляют траекторию, но большую часть станция движется по законам механики.
И еще один вопрос. Вы наблюдаете пролеты МКС в своей местности?
Уважаемая Полина!
С точки зрения механики продолжительномсть полёта МКС между коррекциями целиком и полностью определяется лишь силой аэродинамического сопротивления станции из-за наличия хотя и слабой, но присутствующей атмосферы. Учесть точно влияние сопротивления (коэффициент лобового сопротивления Cx(М), где М число Маха, равное Vорбит./a звука) можно либо при наличии точных аэродинамических продувок станции в сооответствующих сверхзвуковых трубах ЦАГИ, поскольку её форма весьма специфическая и представляет из себя больше летящую птицу с огромными боковыми солнечными панелями - крыльями, сильно влияющими на коэффициент сопротивления, либо просто эмпирически по величине потери орбитальной скорости полёта станции за заданный период времени, что гораздо проще и точнее.
Но от неизбежной потери скорости никуда не деться. Единственный выход - поднять дополнительно высоту высоту полёта станции над Землёй на пару сотен км в область ещё более разряженной атмосферы. Но сверху, как Вы прекрасно знаете, есть ограничение на попадание в область нижней границы пояса Ван-Аллена, в котором крутятся, подобно белке в беличьем колесе, высоко скоростные заряженные частицы, выброшенные Солнцем в виде солнечного ветра, которые сродни вредным фактором атомного взрыва и ничего хорошего не приносящими здоровью космонавтов на станции. Известно, что после сильных солнечных магнитных бурь радиоактивность в поясе возрастает на несколько порядков и держится месяцами на высовом уровне. Что является весьма жёстким ограничением на пилотируемые полёты в открытый космос. Поскольку при пересечении пояса в таком высокоактивном состоянии можно получить смертельную дозу радиации за одно пересечение этого пояса, толщина которого достигает порядка 1-1,5 тыс.км.(по памяти)) При этом надо выбирать особые траектории выхода и входа в пояс ближе к полюсам магнитного поля Земли, где его толщина минимальна.
Поскольку станция и так довольно высоко летает, то остаётся только доставлять периодически дополнительный запас топлива для поднятия орбиты станции за счёт включения двигателей самих пристыковавшихся "грузовиков".
Наблюдениями пролётов не занимаюсь, распределяю свободное время между работой в огороде (в летнее время) и увлечениями (радиолюбительством (собрал себе Hi-Fi усилитель мощности с малыми искажениями (0,002-0.02%), слушаю советскую эстраду и шедевры инструментальной и классической музыки, иногда фотографирую (Canon_SX-50 и FUJIFILM-S9600 - мегазумные компакты), люблю программировать, а в последнее время, увлёкся написанием комментариев, чему очень рад и благодарен Вашему сайту.
Желаю Вам здоровья и успехов в работе.
Георгий. 1.04.2020г 11час 38мин. Время моск.
Георгий, спасибо за оперативный ответ. Ваш комментарий немного подкорректировала (надеюсь, Вы не будете против) в соответствии с дизайном нашего сайта. Часть своего ответа Вам разместила в другом комментарии.
Эти наблюдения занимают всего 3-5 минут несколько раз в месяц, и то далеко не в каждый. Необходимо только точно знать время и место наблюдения. Все, кто первый раз наблюдал (а многие даже не знают, что это возможно) искренне восхищаются, что можно увидеть невооруженным взглядом рукотворную яркую "звезду", да ещё и быстро движущуюся. Бывают моменты, когда светящаяся МКС ярче всех природных настоящих звезд на небе. Равнодушных не бывает.
На нашем сайте расчетами для наблюдения космической станции в Ульяновской области занимается ВИ0540 в своем проекте Наблюдение МКС. В Дубне время наблюдения мало различается от Ульяновска., только поправка на разницу часовых поясов. На мой взгляд, интересно наблюдать реальные траектории космических тел, особенно в сравнении с расчетными.
Законы механики И.Ньютона в современном изложении
и их формулировка в «Началах».
Содержание:
1. Справка о книге И.Ньютона «Математические начала натуральной философии» и её переводе
2. Определения в книге «Начала».
3. ПЕРВЫЙ ЗАКОН ИНЕРЦИИ НЬЮТОНА. СВОБОДНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНЫХ ТЕЛ
3.1. О возможных внешних воздействиях на материальные тела
3.2. Об инерциальных и неинерциальных системах координат
4. ВТОРОЙ ЗАКОН НЬЮТОНА. УСКОРЕНИЕ ТЕЛА ПОД ВОЗДЕЙСТВИЕМ СИЛЫ
5. ТРЕТИЙ ЗАКОН НЬЮТОНА. ВЗАИМОДЕЙСТВИЕ ДВУХ ТЕЛ.
6. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ НЬЮТОНА
7. Описание принципа работы пружинного динамометра и акселерометра
7.1 Устройство динамометра
7.2 Устройство акселерометра
7.3 Описание принципа работы акселерометра
7.4 О колебательном характере процесса измерении ускорения
7.5 Методы снижения колебательности процесса измерения ускорения
7.6. О невозможности измерения акселерометром гравитационного ускорения притягивающей планеты
7.7. Тарировка акселерометра
8. Пример использования акселерометров в системах управления летательными аппаратами
1. Справка о книге И.Ньютона «Математические начала натуральной философии» и её переводе
Первый том «Начал» был представлен Исааком Ньютоном Королевскому обществу в 1686г., а полностью труд Ньютона под названием «Математические начала натуральной философии» (на современном языке - «Математические основы физики») в трёх томах вышел через год, в 1687г. Тираж (около 300 экземпляров) был распродан за 4 года — для того времени очень быстро. Два экземпляра этого редчайшего издания хранятся в России; один из них Королевское общество в годы войны (1943г) подарило Академии наук СССР на празднование 300-летнего юбилея Ньютона.
Далее Вашему вниманию, уважаемый читатель, предлагаются выдержки из книги серии «Великие умы России» Елены Сельцовой «Алексей Николаевич Крылов». Москва 2017г. о выдающемся переводчике «Начал» И.Ньютона на русский язык А.Н.Крылове - механике, математике и кораблестроителе.
В 1914г выпускник-отличник Морской академии Алексей Николаевич Крылов (03.06.1863 – 26.10.1945) (и её будущий профессор, имя которого будет присвоено позже Морской академии), приступает к переводу с латинского (языка для научных публикаций того времени) «Начал» Исаака Ньютона и в 1916г книга была напечатана полностью с дополнениями в оригинальный текст Ньютона более чем 200 замечаний переводчика размером от пары строк до нескольких листов. В этом же году Крылов был избран действительным членом Российской Академии наук, а позже и членом Академии наук СССР.
Сразу по окончании с отличием Академии Крылов был зачислен в Главное гидрографическое управление, где выполняет свой первый научный труд по расчёту делений для нового дефлектора - прибора, измеряющего действующую на компас магнитную силу, заменяющего ручные расчёты поправок к дополнительному устройству, автоматически корректирующему показания компаса с учётом влияния намагниченности металлических корпусов кораблей, сменивших деревянные суда, которые не искажали показания магнитного компаса. Неоднократные крушения в 19 веке металлических кораблей из-за ошибочных показаний компаса, вызванных девиацией показаний, привели к разработке вышеупомянутого прибора коррекции показаний компаса. Крылов изучив предложенный французский вариант «дромоскопа», построенного на основе приближённой формулы девиации и приводящего к значительным ошибкам, предложил на основе точной формулы девиации своего научного руководителя (основоположника учения о девиации И.П.де-Колонга) новый вариант «дромоскопа», который благодаря простоте оказался в 7 раз дешевле французского прибора. По окончании преподавательской деятельности (в 75 лет) он возвращается к научным изысканиям по компасному делу. За эти работы и курс лекций о девиации А.Н. Крылов был удостоен Сталинской премии 1-й степени в 1941г, а в 1943г. ему было присвоено звание Героя Социалистического Труда.
В начале своей научной деятельности Крылов читал, по совету своего научного руководителя, необходимые для работы сочинения Гаусса на латыни. Только тогда будущий академик осознал важность знания этого языка: «Много раз в течение моей жизни и научной деятельности мне с пользой служила латынь… Я свободно разбирался в элементарно простой латыни Эйлера, несколько труднее в превосходной латыни Ньютона и ещё труднее в чисто классической латыни Гаусса и Якоби». По иронии судьбы, Крылов в детстве, обращаясь к отцу с просьбой разрешить учиться на морского офицера в училище, мотивировал свою просьбу нежеланием «зубрить никому не нужные латынь и греческий». Однако из-за развившейся близорукости к моменту окончания училища мечта о флотской жизни с кругосветными путешествиями оказалась неосуществима.
У англичан перевод «Начал» Ньютона есть только в виде подстрочника. В мире нет издания, подобного переводу А.Н. Крылова. Автор стремился не только сохранить смысл подлинника, но и следил за чистотой русского языка, отказавшись от знаменитой жёсткости языка Ньютона. Крылов писал, что «там, где сейчас принято говорить «сохраняет своё состояние движения», в «Началах» можно прочесть «продолжает упорно пребывать в своём состоянии»; на языке Ньютона сила не прикладывается к телу, а «вдавливается» или «втискивается» в него и т.п. Поэтому с целью приближения текста к современному способу изложения «в переводе принята менее выразительная, но общеупотребительная теперь терминология».
В 1916г. в Петрограде вышла книга «Начал» И.Ньютона в переводе профессора А.Н.Крылова под названием «УЧЕНIЕ о ПРЕДѢЛАХЪ, какъ оно изложено у Ньютона». Это единственный случай, когда переводчиком «Начал» стал выдающийся учёный.
Именно в этой книге «Начал» И.Ньютон сформулировал три закона классической механики и закон тяготения ("закон обратных квадратов", как его называл сам Ньютон и который им был опубликован до написания "Начал"), а также изложил свой вариант (независимо от Лейбница) математического анализа бесконечно малых приращений (метод «флюксий» у Ньютона в отличие от метода дифференциального исчисления у Лейбница, утвердившегося в науке вместо «флюксий» Ньютона) и развил метод вариации произвольных постоянных эллиптического движения применительно к анализу движения Луны, так что уравнении Лагранжа были, по-видимому, предвосхищены в книге Ньютона.
Далее приведены небольшие отрывки из предисловия Л.С.Полака к изданию «Начал» в серии «Классики науки» под названием: «Исаак Ньютон Математические начала натуральной философии» под редакцией Л.С.Полака, Москва ,«НАУКА» 1989. Репринтное издание 1936г. 687стр.
« Школьные годы делают ньютонианцами всех людей на нашей планете… Мы впитываем в нашу духовную плоть три аксиомы (закона) Ньютона, его пространство и время, его закон всемирного тяготения и многое другое… Не случайно Лагранж назвал «Начала» «величайшим произведением человеческого ума».
Открытию закона всемирного тяготения в Англии предшествует период волнующих исканий: Гук, всегдашний противник и оппонент Ньютона, Галлей, восторженный поклонник его и Рен, великий архитектор и учёный, в 1684г. втроём обсуждают в Лондоне вопрос о движении тел под действием силы притяжения; здесь Гук заявляет, что у него уже готово решение, но он откладывает сообщение о нём. Время идёт, и Галлей замечает, что мистер Гук «не так хорош, как его слова», и однажды обращается к Ньютону с вопросом: какая должна быть орбита тела, движущегося вокруг центра притяжения под действием силы, обратно пропорциональной квадрату расстояния? Ньютон немедленно отвечает, что это, конечно же, эллипс и что он уже с 1679г. владеет решением задачи. С этого момента и начинается работа Ньютона, приведшая к созданию «Начал».
Знание тогдашней науки и работ современников видно из анализа состава библиотеки Ньютона. В ней 2100 томов по алхимии и химии, математике и физике, естественным наукам, теологии и классической древности.
Универсальность открытой Ньютоном динамической системы была неожиданностью для его современников…
Ньютон не случайно назвал свой великий труд «Математическими началами» . Математика для него была главным орудием в физических исследованиях. Но Ньютон никогда не терял связи с экспериментом, и в этом его сила. Его изумительное искусство в постановке многочисленных опытов заложило основы экспериментального исследования современного типа. Сам Ньютон писал, что тем, чего он достиг «обязан только усердию и упорной мысли».
Великий труд Ньютона и переворот, произведенный им, не следует рассматривать как результат линейного развития более ранних идей. Если в разработке и применении двух первых законов (аксиом) движения у него были предшественники, то третий закон полностью принадлежит Ньютону и никем не оспаривался.
Как известно, Ньютон сформулировал закон тяготения (закон обратных квадратов), определяющий движение небесных тел в классическом пространстве, до того, как написал «Начала», с успехом приложив его к анализу притяжения между Солнцем и планетами. Однако только согласно его третьему закону гравитация не могла далее рассматриваться как некое изолированное свойство, присущее одному центральному телу Солнечной системы. Она должна быть присуща Луне, каждой планете, комете и звезде во Вселенной – мысль, вероятно, одна из глубочайших, когда-либо приходивших человеческому уму…
В заключение необходимо подчеркнуть воистину бесчисленные подтверждения положений, развитых Ньютоном в «Началах». В течение последних десятилетий они получили решающее «космическое» доказательство: достаточно вспомнить о прецизионных экспериментах, поставленных с помощью искусственных спутников Земли и подтвердивших с высокой точностью уравнения Ньютона.»
В начале своей книги Ньютон даёт восемь Определений(I-VIII) и итоговое Поучение:
2. Определения в книге «Начала».
Определение I
« Количество материи (масса) есть мера таковой, устанавливаемая пропорционально плотности и объёму её.»
Это же количество я подразумеваю в дальнейшем под названиями тело или масса. Определяется масса по весу тела, ибо она пропорциональна весу, что мною найдено опытами над маятниками.
*) Примечание Крылова: Ни одно определение Ньютона не вызвало столько критических замечаний и столько толкований. Термин «Количество материи» составляет как бы одно слово «материя», но при дальнейшем развитии науки не удержался и в современной терминологии заменён равносильным ему термином «масса».
Необходимо так же иметь в виду, что в то время при установлении меры для какой-либо величины устанавливалась лишь её пропорциональность другим величинам, от коих эта мера зависит. Тогда не говорили, как теперь (когда делается предположение о принятой единице массы), «площадь прямоугольника равняется произведению его основания на высоту», а говорили «площадь прямоугольника пропорциональна его основанию и высоте».
До Ньютона понятие о массе не вводилось, а рассматривался лишь вес и при старинной терминологии понятно, что плотность не определялась как масса единицы объёма вещества, а говорилось, что плотность тела пропорциональна его весу и обратно пропорциональна его объёму. Имея это в виду, можно ньютоново определение, придерживаясь теперешней терминологии, выразить так:
«Масса есть мера количества вещества, пропорциональная его плотности и объёму»
Определения II
«Количество движения есть мера такового, устанавливаемая пропорционально скорости и массе»
Количество движения целого есть сумма количеств движения отдельных частей его, значит для массы, вдвое большей, при равных скоростях оно двойное, при двойной же скорости – четверное.
Определение III
« Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения.»
Эта сила всегда пропорциональна массе, и если отличается от инерции массы, то разве только воззрением на неё.
От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому «врождённая сила» могла бы быть весьма вразумительно названа «силою инерции». Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко: и как сопротивление и как напор. Как сопротивление – поскольку тело противится действующей на него силе, стремясь сохранить своё состояние; как напор - поскольку то же тело, с трудом уступая силе сопротивляющегося ему препятствия, стремится изменить состояние этого препятствия. Сопротивление приписывается обыкновенно телам покоящимся, напор – телам движущимся.
Но движение и покой, при обычном их рассмотрении, различаются лишь в отношении одного к другому, ибо не всегда находится в покое то, что таковым простому взгляду представляется.
Определение IV
«Приложенная сила есть действие, производимое над телом, что бы изменить его состояние покоя или равномерного прямолинейного движения.»
Сила проявляется единственно только в действии, и по прекращении действия в теле не остаётся. Тело продолжает затем удерживать своё новое состояние вследствие одной только инерции. Происхождение приложенной силы может быть различное: от удара, от давления, от центростремительной силы.
Определение V
«Центростремительная сила есть та, с которою ТЕЛА к некоторой точке, как к центру, отовсюду притягиваются, гонятся или как бы то ни было стремятся.»
Такова сила тяжести, под действием которой тела стремятся к центру Земли, магнитная сила, которою железо притягивается к магниту, и та сила, каковою бы она ни была, которою планеты постоянно отклоняются от прямолинейного движения и вынуждаются обращаться по кривым линиям. Камень, вращаемый в праще, стремится удалиться от вращающей пращу руки, и этим свои стремлением натягивает пращу тем сильнее, чем быстрее вращение, и как только его пустят, то камень улетает.
Силу, противоположную сказанному стремлению, которою праща постоянно оттягивает камень к руке и удерживает его на круге, т.е. силу направленную к руке или к центру описываемого круга, я и называю центростремительной.
Но тело может испытывать воздействия не только со стороны тел, с которыми оно соприкасается. Оно может подвергаться воздействиям также со стороны различного рода силовых полей, возбуждаемых другими телами. Поэтому вопрос сводится к тому, как убедиться в том, что воздействиям со стороны силовых полей тело не подвергается. Брошенное тело, если бы силы тяжести не было, не отклонялось бы к Земле, а уходило бы в небесное пространство по прямой линии равномерно, если бы не было и сопротивления воздуха. Своею тяжестью оно оттягивается от прямолинейного пути и постоянно отклоняется к Земле в большей или меньшей степени, сообразно напряжению силы тяжести и скорости движения.
Увеличивая скорость свинцового ядра, брошенного горизонтально силою пороха из пушки, поставленной на вершине горы, можно по желанию увеличить и дальность полёта и уменьшить кривизну линии, по которой ядро движется, так чтобы заставить его упасть как можно далее от горы и можно было бы окружить всю Землю или даже уйти в небесные пространства и продолжить удаляться до бесконечности. Подобно тому, как брошенное тело может быть отклонено силою тяжести так, чтобы описать орбиту вокруг Земли, так и Луна или силою тяжести, если она ей подвержена, или же иною силою, которая влечёт её к Земле, может быть отклоняема от прямолинейного пути и вынуждена обращаться по своей орбите. Если бы сила была меньше соответствующей этой орбите, то она отклонила бы Луну от прямолинейного пути недостаточно, а если больше, то отклонила бы её более, чем следует, и приблизила бы её от орбиты к Земле. Следовательно, надо, чтобы эта сила была в точности надлежащей величины.
Дело математиков найти такую силу, которая в точности удерживала бы заданное тело в движении на заданной орбите с данною скоростью, и наоборот, найти тот криволинейный путь, на который заданною силой будет отклонено тело, вышедшее из заданного места с заданной скоростью.»
*) Вот так Ньютон вводит, поразившее всех современников, понятие о Динамической системе, или как её часто называют механики "Задача расчёта динамики" движения тела!
3. ПЕРВЫЙ ЗАКОН ИНЕРЦИИ НЬЮТОНА. СВОБОДНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНЫХ ТЕЛ
(Далее, (в кавычках «…») приводятся цитаты из учебника: Сивухин Д.В. Общий курс физики. Том1. Механика 2005г. МФТИ. и из «Начал»И.Ньютона)
В качестве Первого закона движения Ньютон принял закон инерции, высказанный в частной форме еще Галилеем.
Согласно этому закону тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно.
Для примера, приведём, два равноценных варианта Первого закона из «Начал» в переводе А.Н. Крылова:
«Всякое тело продолжает пребывать в своём состоянии покоя или равномерного прямолинейного движения, пока приложенные силы не понудят его изменить это состояние», или как второй вариант этого же перевода:
«Всякое тело удерживает своё состояние покоя или равномерного и прямолинейного движения, поскольку оно не понуждается приложенными силами изменять это состояние».
Такое тело называется свободным, а его движение — свободным движением или движением по инерции. Свободных тел, говоря точно, не существует. Они являются физическими абстракциями. Однако можно поставить тело в такие условия, когда внешние воздействия на него по возможности устранены или практически компенсируют друг друга. Представив себе, что эти воздействия беспредельно уменьшаются, мы и приходим в пределе к представлению о свободном теле и свободном движении.
Итак, всякое тело оказывает сопротивление при попытках изменить величину (модуль) или направление его скорости. Это свойство тел называется инертностью. У разных тел оно проявляется в разной степени. Так, сообщить одно и то же ускорение большому камню значительно труднее, чем маленькому мячику. Мера инертности тела называется его массой, которая пропорциональна количеству вещества в теле. Чем больше масса тела, тем оно инертней и тем труднее изменить вектор скорости этого тела.
В качестве эталона для измерения массы тел условились взять массу определенного тела и считать её равной единице. Тогда массы всех остальных тел определятся однозначно.
В физике в качестве основной единицы массы принят килограмм. Килограмм есть масса эталонной гири из сплава иридия с платиной, хранящейся в Севре (Франция) в Международном бюро мер и весов. Приближенно килограмм равен массе кубического дециметра чистой воды при температуре 4 °С. Тысячная доля килограмма называется граммом».
3.1. О возможных внешних воздействиях на материальные тела
« Здесь, однако, возникает следующая трудность. Как убедиться в том, что тело не подвержено внешним воздействиям? Об этом нельзя судить только по отсутствию ускорений. Нужны какие-то другие независимые способы. Иначе закон инерции потерял бы всякое содержание. Вполне удовлетворительного ответа на этот вопрос не существует.
В отсутствие внешних воздействий мы убеждаемся по отсутствию растягивающих пружин или веревок, которые тянут тело, по отсутствию тел, которые давят на него, т. д.
Все силы, встречающиеся в природе, известные в настоящее время, сводятся к силам гравитационного притяжения, электромагнитным силам, сильным и слабым взаимодействиям. Сильные и слабые взаимодействия проявляются в атомных ядрах и в мире элементарных частиц. Они действуют на малых расстояниях: сильные - на расстояниях порядка 10-13 см, слабые на расстояниях порядка 10-16 см. В макромире, который только и изучает классическая механика, от сильных и слабых взаимодействий можно отвлечься.
Электромагнитные и гравитационные силы, напротив, являются силами дальнодействующими. С расстоянием они убывают медленно. Если это статические силы, то они убывают обратно пропорционально квадрату расстояния. Если же они переменные (электромагнитные волны), то убывание происходит еще медленнее — обратно пропорционально расстоянию. Только благодаря электромагнитным волнам (свет, радиоизлучение, рентгеновское излучение), исходящим от планет, звезд, пульсаров, галактик и пр., мы и знаем о существовании этих небесных объектов. Поэтому нет оснований утверждать, что удаленные источники не возбуждают заметных электромагнитных и гравитационных полей в рассматриваемой нами области пространства. Однако в отсутствие электромагнитных полей всегда можно убедиться, так как они действуют по-разному на положительные и отрицательные заряды, из которых состоят тела. Под действием таких полей возникло бы некоторое разделение положительных и отрицательных зарядов, которое можно было бы обнаружить на опыте. Заряженный шарик, помещенный в одну и ту же точку пространства, двигался бы по-разному в зависимости от того, заряжен он положительно или отрицательно. Все имеющиеся факты не противоречат утверждению, что удаленные тела Вселенной не возбуждают сколько-нибудь заметных статических электромагнитных полей в малых областях пространства (порядка размеров Солнечной системы или Галактики).
О гравитационных полях этого нельзя сказать с той же уверенностью. Но если бы такие поля и существовали, то с ними можно было бы не считаться. Дело в том, что всем телам, независимо от их состава, одно и то же гравитационное поле сообщает в точности одинаковое ускорение. Статическое гравитационное поле удаленных тел Вселенной в малых областях пространства можно считать практически однородным.
Можно ввести систему отсчета, свободно падающую в таком однородном гравитационном поле. На явлениях, происходящих в такой системе отсчета, наличие этого однородного гравитационного поля никак не сказывается. Здесь все происходит в точности так же, как в кабине космического корабля, свободно движущегося в космическом пространстве. В такой кабине космонавты не чувствуют наличия поля тяготения (невесомость)».
*) примечание: см. также ниже раздел 7.6. О невозможности измерения акселерометром гравитационного ускорения притягивающей планеты.
3.2. Об инерциальных и неинерциальных системах координат
« В кинематике выбор системы отсчета не был существенным. Все системы отсчета кинематически эквивалентны. Не так обстоит дело в динамике.
Уже закон инерции с особой остротой ставит вопрос о выборе системы отсчета. Одно и то же движение выглядит по-разному в разных системах отсчета. Если в какой-либо системе отсчета тело движется прямолинейно и равномерно, то в системе отсчета, движущейся относительно первой ускоренно, реально движущееся равномерно тело будет казаться движущимся ускоренно.
Отсюда следует, что закон инерции не может быть справедлив во всех системах отсчета. Без указания системы отсчета он просто теряет смысл. Классическая механика постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчета. Содержание закона инерции, в сущности, сводится к утверждению, что существует по крайней мере одна инерциальная система отсчета.
Попробуем взять гелиоцентрическую систему отсчета, иначе называемую системой Коперника (по имени польского астронома Николая Коперника (1473—1543)). Это есть координатная система, начало которой помещено в центре Солнца (точнее, в центре масс Солнечной системы), а координатные оси являются прямыми, направленными на три удаленные звезды и не лежащими в одной плоскости. Материальными объектами, с помощью которых реализуются эти оси, являются световые лучи, приходящие от звезд в Солнечную систему. Из-за относительного движения звезд углы между координатными осями в системе Коперника не остаются постоянными, а медленно изменяются с течением времени. Однако ввиду колоссальности расстояний до звезд изменения направлений координатных осей происходят настолько медленно, что, как правило, их можно не принимать во внимание. Система Коперника практически является инерциальной системой, по крайней мере при изучении движений, происходящих в масштабе нашей планетной (Солнечной) системы.
Неинерциальность Земной системы отсчета объясняется тем, что Земля, во-первых, вращается вокруг собственной оси и, во-вторых, - вокруг Солнца, т. е. движется ускоренно относительно системы Коперника. Впрочем, оба эти вращения происходят медленно. Поэтому по отношению к громадному кругу явлений происходящих на Земле Земная система отсчета ведет себя практически как инерциальная система. Обычные, сравнительно грубые наблюдения и опыты над движением тел не позволяют обнаружить отступления от инерциальности земной системы отсчета. Для этого требуются более точные и тонкие опыты.
Вот почему при установлении основных законов динамики можно начать с изучения движения тел относительно Земли, отвлекаясь от её вращения, т. е. принять Землю за приблизительно инерциальную систему отсчета.»
*) Примечание: Рассуждения выше относятся, конечно же не к полётам спутников вокруг Земли, а к анализу движения обычных относительно небольших по масштабам расстояний земных тел. Например, при учёте движений, связанных с большими расстояниями, необходим учёт неинерциальности Земли, как, например, влияния силы Кориолиса для рек, или изменение ускорения притяжения на полюсе и экваторе и т.п.
4. ВТОРОЙ ЗАКОН НЬЮТОНА. УСКОРЕНИЕ ТЕЛА ПОД ВОЗДЕЙСТВИЕМ СИЛЫ
« Общие законы движения Ньютон сформулировал с использованием понятия СИЛЫ. Представление о силе возникает в связи с ощущением мускульного усилия, которое у нас возникает при поднятии тяжелых тел или при приведении их в движение.
Под силой в механике понимают всякую причину, изменяющую скорость тела. В инерциальной системе отсчета производная от скорости материальной точки по времени представляется уравнением.
Эти уравнения выведены при условии, что масса тела является постоянной величиной и независящей от скорости тела.
m * (dv/dt) = F; или, в другом виде: (dv/dt) = F / m; (4.1)
m * (d2r/dt2) = F; или, в другом виде: (d2r/dt2 ) = F / m; (4.2)
Величина F называется результирующей (геометрической суммой всех сил по правилу параллелограмма) силой, действующей на рассматриваемую материальную точку. Очевидно, что сила F является вектором (обладает направлением в пространстве), поскольку она равна производной вектора скорости по времени, или же второй производной от координаты тела.
Таким образом, в инерциальной системе отсчета производная от скорости (или ускорение) равна действующей на неё результирующей силе, отнесённой к массе тела. Это утверждение называется вторым законом Ньютона, а соответствующие ему уравнения — уравнениями движения материальной точки.
Конечно, если движение тела (материальной точки) известно, т. е. известны ее координаты как функции времени t, то простым дифференцированием по времени (t) можно определить величину действующей силы (представляющей собой геометрическую сумму всех сил, действующих на тело) как функцию того же времени.»
В связи с отсутствием понятия ускорения второй закон у Ньютона формулируется в виде изменения количества движения, т.е. изменения величины произведения массы на скорость тела (при постоянстве массы тела) так:
«Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой , по которой эта сила действует».
Примечание Крылова: В непосредственной связи со вторым законом находится Лемма X, в которой показывается, что в пределе для бесконечно малых промежутков времени изменения скорости тела, а значит, и количества движения, производимые силою, пропорциональны времени. Эта Лемма в связи со вторым законом и с понятием об «ускорении» в его теперешнем смысле, и устанавливает пропорциональность силы ускорению.
5. ТРЕТИЙ ЗАКОН НЬЮТОНА. ВЗАИМОДЕЙСТВИЕ ДВУХ ТЕЛ.
« Силы взаимодействия двух материальных точек равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки. Одну из сил, согласно Ньютону, иногда называют действием, а другую — противодействием.
Формулируют третий закон следующим образом:
Всякому действию соответствует равное и противоположно направленное противодействие.
Следует, однако, заметить, что «действие» по своей физической природе ничем не отличается от «противодействия». Если действующая сила обусловлена деформацией, всемирным тяготением или наличием электрического поля, то и противодействующая сила обусловлена тем же самым. Так, тяжелое тело, лежащее на столе, давит на стол, испытывая со стороны стола противоположно направленное противодавление. Действие — давление камня на стол — обусловлено деформацией камня, противодействие давление стола на камень — обусловлено деформацией стола. В основе подразделения сил на «действующие» и «противодействующие» лежит представление об активных телах, производящих действие, и пассивных телах, оказывающих противодействие.
Так, если лошадь тянет телегу, то активным телом, производящим действие, будет лошадь, а пассивным телом, оказывающим противодействие, — телега.
Однако подразделение тел на активные и пассивные можно провести далеко не всегда. Например, когда Солнце и планета притягиваются друг к другу силами всемирного тяготения, то в этом взаимодействии они выступают совершенно равноправно, и нельзя указать, какое из этих взаимодействующих тел является активным, а какое пассивным. Какую из сил назвать действием и какую противодействием - это в большинстве случаев вопрос соглашения. »
Формулировка Третьего закона у Ньютона:
«Действию всегда есть равное противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.»
Если какое-нибудь тело, ударившись о другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своём собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга постоянно равны. От таких взаимодействий всегда происходят равные изменения не скоростей, а количеств движения, предполагая, конечно, что тела никаким другим усилиям не подвергаются. Изменения скоростей, происходящие также в противоположные стороны, будут пропорциональны массам тел, ибо количества движения получают равные изменения. Этот закон имеет место и для притяжений.
И вот весьма важное Следствие IV, посволяющее выбрать точку для размещения начала системы координат, в которой планируется рассчитывать траектории движения различных тел, т.е. решать Динамическую задачу, как её поставил сам Ньютон выше в ОпределенииV.
Следствие IV
«Центр тяжести системы двух или нескольких тел от взаимодействия тел друг на друга не изменяет ни своего состояния покоя, ни движения; поэтому центр тяжести системы всех действующих друг на друга тел (при отсутствии внешних действий и препятствий) или находится в покое, или движется равномерно и прямолинейно.»
Следовательно, по отношению к центру тяжести системы нескольких тел имеет место тот же самый закон сохранения состояния покоя или равномерного и прямолинейного движения, как и для одного тела. Таким образом, поступательное количество движения отдельного ли тела или системы тел надо всегда рассчитывать по движению центра тяжести их.
*) Примечание: В современном механике центр тяжести заменяется на более точное понятие центра масс системы, или центра инерции системы(см., например, книгу М.А. Айзермана "Классическая механика", стр.73).
Центр тяжести и центр инерции системы тел практически совпадают при условии размещения рассматриваемых тел в однородном внешнем поле ускорения от притяжения планетой или Солнцем, т.е. постоянном по величине внещнего ускорения и действии его на все тела системы по параллельным линиям, проще говоря, при постоянном векторе внешнего ускорения. Использование центра инерции системы тел Солнечной системы для размещения в нём начала инерциальной систем отсчёта (это, так называемая, барическая система (барсистема)) будет весьма правильным решением для избавления её от всех вращательных движений, присущих даже самому Солнцу из-за его вращении вокруг центра масс Солнечной системы, расположенныму, иногда даже вне пределов сферы самого Солнца (например, при "параде планет", когда они выстраиваются в одну линию относительно Солнца и совместным количеством движения сильнее всего смещают центр инерции относительно центра масс Солнца.
Следствие V
« ОТНОСИТЕЛЬНЫЕ ДВИЖЕНИЯ друг по отношению к другу тел, заключённых в каком-либо пространстве, ОДИНАКОВЫ, покоится ли это пространство или движется равномерно и прямолинейно без вращения.»
Следствие VI
« Если несколько тел, движущихся как бы то ни было друг относительно друга, будут подвержены действию равных ускоряющих сил, направленных по параллельным между собою прямым, то эти тела будут двигаться друг относительно друга так же, как если бы сказанные силы на них не действовали.»
Так как эти силы, действуя на все тела одинаково (соответственно массам движущихся тел) и по направлению параллельным, будут сообщать всем телам одинаковые скорости (по второму закону), то они ни в чём не изменят ни положений, ни движений тел друг относительно друга.
*) Примечание:
Именно это Следствие VI, было использовано автором данного комментария (метод "обращения движения в обратную сторону" относительно вектора внешнего ускорения от Солнца, т.е. его векторное вычитание из центров масс для всех рассматриваемых тел) для обоснования перехода расчёта движения Луны относительно Земли из Солнечной системы координат (задачи "трёх тел") в Земную (задаче "двух тел"), естественно с учётом некоторой фактической неодинаковости как по величине внешнего ускорения Солнца, так и небольшой их непараллельности для Луны и Земли, да к тому же и при наличии годового вращения гравитационного поля Солнца относительно Земной группы тел. Однако, за счёт применения метода учёта ТОЛЬКО ПРИРАЩЕНИЙ (а неполной величины!) от внешнего возмущающего ускорения Солнца, т.е. компенсации влияния этой неоднородности относительно начала Земной системы отсчёта практически удалось скомпенсировать влияние всех этих отклонений от идеальных условий, оговоренных в данном СледствииVI. Кроме того начало системы отсчёта (с учётом того, какие тела рассматриваются) также размещается ещё и в центре инерции рассматриваемой системы тел (в её барцентре, см. выше примечание к Следствию IV).
6. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ НЬЮТОНА
« Ньютон сформулировал закон всемирного тяготения (его закон "обратных квадратов"), согласно которому любые два тела (материальные точки) притягиваются друг к другу с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними:
F = G * (M*m) / r2 ; (6.1)
Такие силы называются гравитационными или силами всемирного тяготения.
Коэффициент пропорциональности G, входящий в формулу и введённый позже в употребление, один и тот же по величине для всех тел. В этом смысле коэффициент G является универсальной постоянной. Это одна из важнейших мировых постоянных, называемая гравитационной постоянной.
Измерения G современными методами привели к следующему результату на сегодняшний день:
G = (6,6725 ±0,0005) * 10-8 дин * см2 * г-2 = (6,6726±0,0005)-10-11 H * м2 * кг-2.
Гравитационная постоянная, как мы видим, весьма мала. Поэтому и гравитационные взаимодействия между обычными телами, даже считающимися большими с общежитейской точки зрения, ничтожно малы. Нетрудно подсчитать, что два точечных тела с массами по одному килограмму, находящиеся на расстоянии 1 м друг от друга, взаимно притягиваются с силой F = 6,67 • 10-11 Н = 6,67 • 10-6 дин. »
Для тел, находящихся в гравитационной области Земли, закон всемирного тяготения запишется так:
Fпр.= G * (MЗемли *mтела) / (r тело-цмЗемли) 2; (6.2)
где r тело-цмЗемли - расстояние от центра масс тела до центра масс Земли.
Логично объединить три параметра в один, называемый ускорением земного притяжения:
g (r) = G * MЗемли / r тело-цмЗемли 2 ; (6.3)
И тогда сила притяжения Земли примет простое выражение по типу 2-го закона Ньютона для сил.
Fпр. = g (r) * m тела; (6.4)
Для тел, расположенных на поверхности Земли (уровне океана), ускорение земного притяжения было получено опытным путём для общепринятого среднего радиуса Земли (r Земли = 6,371*106 м).
g 0 = G * MЗемли / r цмЗемли 2 = 9,78 (на экваторе) или 9,81 (на полюсе)м/сек2 ≈9,80 м/сек2 (6.5)
Как следует из всемирного закона тяготения (6.1) ускорение земного притяжения обратно пропорционально квадрату расстояния между телом и центром массы Земли.
Логично избавиться при определении ускорения притяжения g(r) от произведения двух неизменных параметров (G * MЗемли), поделив выр. 6.3 на 6.5 .
В итоге, получено выражение для ускорения гравитации в околоземном пространстве.
g = g 0 * (r цмЗемли / r тело - цмЗемли )2 ; (6.6)
После подстановки расстояния до центра масс Земли (r тело-цмЗемли) в виде суммы высоты полёта над уровнем океана (rg0) (т.е. расстояние от тела до высоты определения значения g0) и среднего радиуса Земли (rЗемли) получим более подходящее для орбитальных полётов выражение для g :
g(rg0) = g 0 * ( r цмЗемли / (r цмЗемли + rg0 ) )2 ; (6.7)
где: g 0 ≈ 9.8 м/сек2 , rg0 [м] – расстояние (оно же высота полёта над океаном) от тела до среднего уровня (поверхности) Земли, на которой и было определено ускорение g 0, средний радиус Земли - rцмЗемли = 6,3781*106 м.
7. Описание принципа работы пружинного динамометра и акселерометра.
При описании 2-го закона было введено понятие СИЛЫ, которое возникает у человека в связи с ощущением мускульного усилия, которое он должен развить при поднятии разных по массе тел или при приведении их в движение из состояния покоя. Для объективного измерения величины силы можно, например, использовать пружинные весы, называемые в физике динамометром (измерителем силы).
На рис.1 показан более сложный прибор, называемый акселерометром, который тоже построен на базе пружины, но на нижнем конце пружины у него подвешено тело, определённой и постоянной массы для данного прибора.
7.1 Устройство динамометра.
Динамометр устроен ещё проще, чем акселерометр. К нижнему свободному концу пружины вместо измерительного тела подсоединена жёсткая тяга, выведенная через отверстие в дне корпуса наружу, к которой можно приложить внешнее усилие, например, нажать ею на какой-либо тело или же подвесить груз определённой массы, а, следовательно, и определённой силы. Например, в условиях гравитации на поверхности Земли сила притяжения груза к Земле будет равна в соответствии со 2-м законом
чем на Земле, и динамометр покажет для гири массой в 1 кг измеренное значение силы веса ~ 0,17кГ на Луне вместо 1кГ на Земле. А человек массой 100кг на Луне будет давить на поверхность Луны с силой ~ 17кГ, вместо 100кГ в условиях Земли. (Извиняюсь за применение устаревшей системы единиц (1кГ-силы вместо 9,81Ньютонов), но так как-то привычнее для нашего поколения.)
7.2 Устройство акселерометра.
Для летательных аппаратов (сокращённо ЛА) необходимо уметь определять на борту ЛА собственную траекторию полёта, скорость и ускорение движение аппарата относительно поверхности Земли., чтобы долететь в нужную точку над поверхностью Земли. Для этого система управления ЛА снабжается тремя датчиками ускорений, называемыми блоком акселерометров с осями чувствительности, направленными строго по трём осям связанной системы ЛА. Интегрирование показаний акселерометров (после их предварительного проектирования из связанной системы в невращающуюся систему координат с использованием показаний углов ориентации связанной системы относительно невращающейся, получаемых от дополнительных гироскопических датчиков углов) позволяет определить сначала величины проекций текущего ускорения центра масс ЛА, которые непрерывно интегрируются по времени с целью получения составляющих скоростей, а параллельно с этим идёт интегрирование самих составляющих скоростей, позволяющее рассчитать уже декартовые координаты ЛА, т.е. его траекторию полёта в этой невращающейся системе отсчёта.
Акселерометр представляет собой дальнейшее развитие динамометра, к которому в нижней части пружины жёстко прикреплено измерительное тело определённой и постоянной массы (далее просто тело) и помещённое (в отличие от динамометра) в полностью закрытый и герметичный корпус прибора. Принципиальная разница между ними состоит в том, что динамометр, обычно используют для измерения сил в статических неускоренных режимах, например, определения силы веса различных тел, т.е. их взвешивания в быту или для измерения сил в физических опытах. А акселерометр применяют для измерения линейных ускорений движущегося объекта, т.е. в динамических режимах полёта ЛА, когда динамометр дополнительно снабжают небольшим измерительным телом постоянной массы, подвешенным на измерительной пружине, что позволяет производить измерения величины силы (по величине растяжения пружины), действующей на это измерительное тело при РАЗНЫХ величинах внешнего ускорения, сообщаемых корпусу прибора в виде геометрической суммы силы тяги двигателя и аэродинамического сопротивления атмосферы Земли. При этом измеренная величиа силы, приложенной к постоянной по величине измерительной массе, пропорциональна ускорению, действующему на акселерометр в соответствии со вторым законом Ньютона, что и означает измерение акселерометром величины внешнего ускорения, действующего на корпус прибора.
Внешнее измеряемое ускорение объекта сообщается корпусу акселерометра, закреплённого на движущемся объекте в нужном для измерения направлении, а тело, подвешенное на пружине, сопротивляясь по закону инерции этому разгону, вынуждено из-за упругой силы всё более растягивающейся пружины двигаться, в итоге, с тем же внешним ускорением, что и корпус прибора. При этом по установившейся величине растяжения пружины можно, как и в динамометре, определить по шкале величину силы, приложенной к измерительному телу прибора, а поделив измеренную силу на известную постоянную измерительную массу тела, подвешенного к пружине, вычислить величину ускорения тела, которое в установившемся режиме соответствует величине внешнего ускорения, сообщаемого корпусу прибора за счёт его механической связи с корпусом ЛА. Реально градуровка акселерометра выполнена не в величинах силы, а в величинах ускорения, а иногда и в величине перегрузки, показывающей во сколько раз измеренное ускорение превышает ускорение на поверхности Земли(=9,81 м/сек2).
На рис.1 и схематично показано устройство пружинного акселерометра. Далее для простоты будем называть акселерометр просто прибором. Каким же способом формируется в приборе сигнал об ускорении? Величина смещения пружины (Х) может быть измерена в акселерометре, например, потенциометрическим способом, с помощью жёстко закреплённого на подвешенном к пружине теле электрического металлического контакта (щётки), скользящего по проволочному линейному потенциометру, закреплённому на корпусе прибора и запитанному постоянным эталонным напряжением. При этом со скользящего контакта может быть получено измеренное напряжение U Wi измер., пропорциональное величине растяжения пружины (Х) под действующим на тело ускорением и снятое с потенциометра напряжение можно пересчитать либо в единицы линейного ускорения, например, в [м/сек2], либо в уровнях перегрузки, n =Wi измер / g0, где g0=9,81м/сек2 – ускорение свободного падения на уровне поверхности Земли. Уровень перегрузки (n) показывает во сколько раз ускорение, сообщаемое телу, превышает ускорение свободного падения, иначе говоря, во сколько раз сила от внешнего ускорения, действующая на тело, превышает обычную земную силу притяжения.
7.3 Описание принципа работы акселерометра.
Если корпус прибора покоится, т.е. не движется с линейным ускорением вдоль оси пружины прибора (назовём её измерительной осью прибора, вдоль которой производится измерение ускорения), то его пружина находится в свободном ненапряжённом (не сжата и не растянута) состоянии, тело прикреплённой к ней также сохраняет состояние покоя и показания прибора нулевые (нет ускорения). Когда ЛА начнёт разгон для набора скорости за счёт включения тяги двигателя на максимальный режим центр масс ЛА и все тела на борту аппарата начнут двигаться с ускорением, например, величиной Wi изм., то корпус прибора, с измерительной осью выставленной вдоль продольной оси ЛА, также начнёт ускоряться с этим же самым ускорением, поскольку прибор жёстко закреплён на ЛА. Тело, повешенное на пружине и стремящееся сохранить свою скорость по 1-му закону инерции, начнёт также разгоняться в сторону этого ускорения за счёт всё большего растяжения пружины и, соответственно, возрастающему усилию растянутой пружины в соответствии с законом Гука (по выр.4.2).
Через небольшой интервал времени (так называемую "постоянную времени прибора"), когда ускорение тела прибора сравняется с ускорением его корпуса величина растяжения пружины Х покажет на шкале пружины ускорение, измеренное прибором (см. выр.4.3).
Wтела = Wi изм. = Fпр / mтела = (k * X) / mтела ; (4.3)
Из 4.3 следует, что измеряемое ускорение однозначно определяется величиной растяжения пружины X (см. выр.4.4), поскольку коэффициент жёсткости пружины (k) и масса измерительного тела прибора (mтела) являются конструктивной постоянной прибора (k констр). А величины коэффициента жёсткости пружины и массы тела выбираются разработчиками прибора такими, чтобы обеспечить прибору требуемый диапазон измеряемых ускорений с учётом ограничений на длину прибора, а значит и на максимальный диапазон растяжений для пружины (Хмин-Х мах).
Wi изм. = (k / mтела ) * X = k констр * Х; (4.4)
7. О колебательном характере процесса измерении ускорения
Рассмотрим работу прибора при скачкообразном появлении внешнего УСКОРЕНИЯ, сообщаемого корпусу прибора скачком от нуля до некоторого значения (Wi измер.) постоянной величины (для простоты рассуждений), что имеет место, например, при включении двигателя самолёта на полную тягу в момент начала разгона самолёта.
Корпус прибора (будучи закреплённым на объекте, например, вдоль продольной оси самолёта) вместе с верхней точкой подвеса пружины к корпусу прибора начнёт двигаться с приложенным внешним ускорением (Wi измер.), однако тело подвешенное к противоположному свободному концу пружины в соответствии с 1-м законом инерции будет стремиться сохранить своё свободное неускоренное состояние покоя и расстояние между измерительным телом и точкой подвеса прижины к корпусу прибора начннёт возрастать, но при этом растяжение пружины Х начнёт увеличиваться, что приведёт к появлению в точке соединения пружины с телом соответствующей нарастающей упругой силы пружины: Fпр = k * Х , которая приведёт в соответствии со 2-законом Ньютона к появлению УСКОРЕНИЯ у тела, т.е. к его ускоренному движению в направлении упругой силы пружины:
(d2Х/dt2) = Fпр / mтела = (k * Х) / mтела (4.5)
При этом первый интеграл от этого ускорения даст скорость движения (V=dХ/dt) тела, а второй интеграл – величину отклонения пружины от её свободного состояния (Х).
Процесс увеличения растяжения пружины (Х) будет продолжаться пока всё возрастающая упругая сила пружины НЕ СООБЩИТ телу, подвешенному на пружине ускорение равное внешнему измеряемому ускорению (Wi измер.) . Когда внешнее ускорение корпуса прибора и ускорение тела, подвешенного на пружине, совпадут, то по величине растяжения пружины Х с учётом тарировки пружины (об этом несколько ниже) можно получить данные о величине внешнего ускорении Wi измер. Назовём эту величину растяжения пружины балансировочным значением измеренного внешнего ускорения (ХWiизм), а соответствующее ему напряжение сигнала прибора, снимаемое со щётки потенциометра, U Wi измер.
Однако процесс растяжения пружины в момент сравнивания внешнего ускорения с ускорением тела может и НЕ прекратится, а продолжиться и будет носить далее характер слабо затухающих синусоидальных колебаний относительно балансировочного значения ХWiизм. Колебательность тела на пружине появится, если в конструкцию прибора не будет заложено специальных мер демпфирования этих колебаний (см. Рис. 2 для случая с kдемпф1=0).
Причина этих колебаний в том, что незадемпфированное тело не остановится в момент совпадения ускорений корпуса и тела прибора, а продолжит движение в ту же сторону внешнего ускорения из-за набранной к этому моменту скорости тела (см. выше упоминание о первом интеграле от ускорения тела, равным скорости движения тела V) и будет в соответствии с 1-м законом инерции по-прежнему продолжать увеличивать растяжение пружины Х по инерции с набранной им скоростью. Теперь уже добавочная сила пружины из-за её дополнительного растяжения (Х-ХWiизм) начнёт процесс гашения этой скорости до нуля. После того как дополнительное растяжение пружины, вызванное инерцией тела за счёт набранной скорости, остановит тело, обнулив его скорость, оно начнёт своё ускоренное движение в обратную сторону к положению балансировочного значения (ХWiизм), потому что пружина будет растянута сверх балансировочного положения и избыточное растяжение пружины (Х >ХWiизм), которое погасило скорость движения тела до нуля, продолжит её уменьшать, вызвав рост скорости уже в обратном направлении. На обратном пути тело также может проскочить балансировочное положение ХWiизм, поскольку опять может накопить какую-то скорость в процессе ускоренного движения к положению равновесия, равную интегралу от ускорения, и процесс колебаний продолжится. Колебания измерительного тела смогут затухнуть ТОЛЬКО при наличии сил, тормозящих скорость перемещения тела, например, силы трения тела о стенки корпуса прибора.
7.5 Методы снижения колебательности процесса измерения ускорения
Для борьбы с колебательным характером переходного процесса от одного уровня измеряемого ускорения к другому новому значению, необходимо приложить к колеблющемуся телу дополнительную силу, тормозящую скорость его движения и пропорциональную величине скорости, т.е. демпфирующую (гасящую скорость тела) силу, выражаемую формулой:
Fдемпф.= - kдемпф * V; (4.6)
где: минус означает, что демпфирующая сила всегда направлена противоположно вектору скорости.
Если поделить демпфирующую силу на массу тела, то, в соответствии со 2-м законом получим величину ускорения (см. 4.7), гасящего избыточную скорость движения тела, что нам и нужно для демпфирования колебаний тела относительно балансировочного положения.
Wдемпф.= - (kдемпф *V) / m тела; (4.7)
Таких тормозящих сил есть немало в природе, например, это всем известная СИЛА ТРЕНИЯ измерительного тела о стенки цилиндра, относительно которых тело скользит и испытвает тормозящее влияние от силы трения. Однако технически сложно подобрать стабильную по условиям эксплуатации величину требуемого коэффициента демпфирования (kдемпф) для сил трения. Можно воспользоваться также СИЛОЙ ВОЗДУШНОГО ДЕМПФИРОВАНИЯ, когда воздух, заключённый с двух сторон от измерительного тела в герметичной области перемещения тела при движении тела сжимается в области, на которую надвигается измерительное тело и начинает перетекать в соседнюю высвобождаемую телом область с разряжением воздуха через специально спрофилированные продольные шлицы с определённой калиброванной площадью. При этом тело выполняет роль поршня сжимающего воздух и чем меньше площадь щели для перетекания воздуха тем сильнее сжимается воздух и растёт сила, противодействующая перемещению тела, иначе говоря тем больше значение коэффициента демпфирования kдемпф. Вспомните, например, резкий рост ваших усилий при попытке увеличения скорости накачивания велосипедным насосом.
Регулируя величину площади сечения для перетекания воздуха между полостями разделёнными измерительным телом) можно подобрать такое значение kдемпф у прибора, при котором переходный процесс будет носить быстрозатухающий колебательный характер и даже апериодический, т.е. плавно подходящий к значению ХWiизм (без перерегулирования), т.е. Х(t) =< ХWiизм. (см., например, на Рис.2 процесс при kдемпф3).
Однако, у всех без исключения способов демпфирования есть общий неизбежный недостаток, связанный с тем, что введение дополнительных сил демпфирования СНИЖАЕТ скорость растяжения пружины (dX/dt) в сравнении с вариантом без демпфирования (kдемрф=0). Поэтому время выхода на момент измерения, когда Х ~= ХWiизм, (т.е. величина постоянной времени акселерометра, которую желательно иметь как можно меньше для снижения запаздывания при управлении подвижными маневрирующими ЛА типа зенитных ракет) будет несколько больше, чем при слабозатухающем процессе.
Но и показания слабозатухающего переходного процесса (с kдемпф1=0) нам вовсе не нужны из-за их замусоренности свободными колебаниями измерительного тела не имеющими ничего общего с реальным измеряемым ускорением. Апериодический процесс измерения (с kдемпф3) весьма затянут по времени нарастания выходного сигнала и также вносит свои искажения, состоящие в занижении показаний относительно реального измеряемого ускорения. При интенсивном входном знакопеременном измеряемом ускорении его показания будут сильно занижены относительно реального измеряемого ускорения.
В итоге, на практике выбирают обычно вариант с kдемпф=kдемпф2 с небольшим забросом в 5-10% от ступенчатого входного уровня измеряемой величины (кривая синего цвета) и обладающий неплохой средней скоростью нарастания выходного сигнала при некоторой неизбежной дополнительной потере в быстроте реакции прибора на входное ускорение (небольшом росте постоянной времени запаздывания) мы получаем лучшую точность измеренного ускорения, менее «засорённую» паразитными собственными колебаниями измерительного тела в переходном процессе измерения. (сравните три процесса на Рис.2 ).
Можно также привести ещё один пример уже электромагнитного демпфирования колебаний, когда электропроводящая пластинка, закреплённая на теле акселерометра будет перемещаться вместе с ним без физического контакта над постоянным линейным магнитом, закреплённым в корпусе прибора. При относительном перемещении в пластинке за счёт поля магнита в ней будут наводиться токи (так называемые токи Фуко), которые взаимодействуя своими полями с полем внешнего постоянного магнита будут тормозить скорость относительного перемещения пластинки над магнитом. Этот метод демпфирования часто используют в стрелочных электроизмерительных приборах для демпфирования колебаний измерительной стрелки.
7.6 О невозможности измерения акселерометром гравитационного ускорения притягивающей планеты.
Как уже отмечалось выше, акселерометр принципиально не способен измерять ускорение, вызванное действием гравитации на прибор, т.к однородное гравитационное поле, воздействуя ОДИНАКОВО на все элементарные массы прибора, сообщает ОДНО И ТО ЖЕ УСКОРЕНИЕ всем частям прибора и поэтому НЕ ВОЗНИКАЕТ НИКАКИХ РАЗНОСТНЫХ СИЛ между подвижной и неподвижными частями прибора, а поскольку нет разностных сил, то и нет перемещений, нет растяжения пружины и нет никаких показаний прибора.
Поэтому УСКОРЕНИЕ свободного падения космического корабля на какую-либо планету или Солнце под действием их гравитационного притяжения НЕ МОЖЕТ БЫТЬ измерено на борту корабля никакими внутренними приборами без привлечения какой-либо дополнительной внешней информации о притягивающей нас планете или звезде.
Измерить в космическом полёте гравитационное ускорение от ближайшей планеты можно только с првлечением на помощь ВНЕШНЕЙ информации, например, при локации планет радиолучом с получением отраженного сигнала и выделением информации о скорости сближения с притягивающей планетой и вычислении производной от скорости для определения ускорения в направлении на планету, либо с применением обработки оптических данных по временному параллаксу центра притяжения на фоне неподвижных звёзд.
В режиме «свободного падения» физическое ощущение состояния «невесомости» человеком никак не будет зависеть, как и у акселерометра, от самой величины гравитационного ускорения будь оно величиной 1*g (при полёте вокруг Земли в орбитальной станции) или, например, 25*g (при свободном падении на Юпитер).
Это поразительный случай воздействия на человека гравитационной ускорения от воздействия массовой силы притяжения, когда он может лететь с любым по величине линейным ускорением, не ощущая никакой физической нагрузки от величины этого ускорения на свои внутренние органы, а находясь лишь в сотоянии лёгкой «невесомости». Поскольку человек при свободном падении к притягивающему центру планеты, как и акселерометр, НЕ испытывает действия дополнительных разностных внутренних сил, поддерживающих внутренние органы человека относительно его скелета в нужном положении, (например, как брюшная мышечная диафрагма удерживает верхнюю массу органов человека от их опускания вниз к тазу под действием сил притяжения на поверхности Земли), поскольку все его органы и скелет летят с одинаковым гравитационным ускорением и нулевыми относительными скоростями.
Практика показала, что максимально-допустимое для здоровья человека ускорение от внешних негравитационных сил, например, от аэродинамической подъёмной силы, при совершении самолётом интенсивных манёвров уклонения, составляет порядка (8-12)*g даже для тренированных лётчиков (и то в течение нескольких секунд) с использованием специальных противоперегрузочных костюмов. Естественно, наибольшую перегрузку человек может выдержать в лежачем положении относительно вектора действия перегрузки в направлении грудь-спина, т.е. в направлении, перпендикулярном позвоночнику тела, а не вдоль его, поскольку при этом величина возможных смещений внутренних органов при появлении в органах сил, противодействующих большим перегрузочным силам, гораздо меньше, чем в направлении вдоль позвоночника и тем самым снижается величина опасных больших относительных растяжений внутренних органов, могущих привести к разрыву тканей внутренних органов.
7.7 Тарировка акселерометра
Несмотря на то, что акселерометр не может в принципе измерять ускорение от действия гравитации, однако, если его поставить продольной осью вертикально на поверхность Земли, то он покажет ускорение, численно равное гравитационному ускорению g0 = 9.8 м/сек2 , правда, направленному в другую сторону, т.е. вверх, хотя при этом корпус прибора покоится на Земле с нулевым истинным ускорением!
Кажущийся парадокс объясняется тем, что акселерометр при этом измеряет не ускорение гравитации, а ускорение от ДРУГОЙ СИЛЫ – СИЛЫ ОПОРЫ корпуса на Землю, которая численно равна силе притяжения к Земле в соответствии с 3-им законом Ньютона , т.к. тело находится в покое на поверхности земли и обе силы друг друга уравновешивают. Однако из двух взаимно-уравновешенных сил прибор может реагировать ТОЛЬКО на одну из сил – на реакцию опоры Земли и измеряет её величину, передаваемую от корпуса прибора через верхнюю точку подвеса на пружину, идущую к измерительному телу, т.е. для тела акселерометра реакция опоры земли является ВНЕШНЕЙ негравитационной силой, ускорение от которой он и измеряет.
И, наоборот, если акселерометр начнёт свободно падать с некоторой высоты под действием только одной гравитационной силы притяжения Земли, то пружина его примет своё несжатое свободное ненапряжённое состояние и прибор покажет НУЛЕВОЕ ускорение, поскольку все элементарные массы частей прибора испытываю ОДНО И ТО ЖЕ ускорение свободного падения, но при этом НИКАКИХ РАЗНОСТНЫХ УСКОРЕНИЙ между корпуса прибора и его измерительным телом НЕТ, то и измерить ускорение он не может, хотя весь прибор пребывает в состоянии свободного падения под ДЕЙСТВИЕМ ОДНОЙ СИЛЫ ПРИТЯЖЕНИЯ Земли и падает с ускорением свободного падения, равным g, а показания его будут всё равно нулевыми, не зависящими от величины реального гравитационного ускорения свободно падающего тела.
В условиях полёта над Землёй эту ошибку в показаниях ВЕРТИКАЛЬНОГО ускорения на 1*g компенсируют довольно просто за счёт программного вычитания из измеренного вертикального «кажущегося» ускорения расчётной величины ускорения g(h) с учётом её зависимоcти от высоты полёта над Землёй (см выр.6.7).
Немного о тарировке показаний акселерометра.
Для точной тарировки акселерометра в широком диапазоне измеряемых ускорений можно использовать, например, вращающуюся центрифугу, предварительно направив измерительную ось акселерометра точно на ось вращения центрифуги, и замеряя при этом сигнал напряжения с акселерометра и ставя ему в соответствие расчётную величину центростремительного ускорения, определяемую по известной формуле:
Wцентр.= Ω2 * R;
где: Ω - угловая скорость вращения центрифуги в [рад/сек], а R – расстояние в [м] от оси вращения до акселерометра, а точнее - до центра масс измерительного тела, подвешенного на пружине.
Кроме того, прибор можно промасштабировать не в только единицах линейного ускорения в [м/сек2], а и в уровнях перегрузки, n = Wi измер / g0, где g0 = 9,81м/сек2 – ускорение свободного падения на уровне поверхности Земли. Уровень перегрузки (n) показывает во сколько раз измеренное ускорение превышает ускорение свободного падения, или иначе говоря, во сколько раз сила от внешнего ускорения, действующая на тело, превышает нормальную силу веса земной гравитации.
При этом вполне допустим и нелинейный характер тарировочной кривой с отступлением от области линейной упругости пружины при крайних значениях ускорений, лишь бы характеристики жёсткости пружины были стабильны и повторяемы при повторных циклах измерений (т.е. при отсутствии остаточных деформаций у измерительной пружины прибора) и тогда точное измеренное значение ускорения будет определено с учетом его тарировочного графика.
8. Пример использования акселерометров
в системах управления летательными аппаратами.
Для измерения величины ускорения, с которым движется вдоль заданного направления какой-либо объект, например, самолёт или ракета, следует использовать акселерометр, измеряющий линейное ускорение вдоль своей измерительной оси.
Для определения полного вектора ускорения объекта, летящего в трёхмерном пространстве, например, самолёта или ракеты, необходимо и достаточно расположить ТРИ датчика ускорений по трём декартовым взаимно-перпендикулярным осям (OX1, OY1, OZ1) , связанными с телом, (см.рис.3). Этих 3-х датчиков будет необходимо и достаточно, чтобы определить пространственную траекторию движения данного объекта в 3-мерном пространстве, и его полную СКОРОСТЬ и УСКОРЕНИЕ относительно земной системы координат (с.к.) .
При этом надо только предварительно пересчитать (спроектировать) измеренные ускорения из связанной системы координат объекта (OX1, OY1, OZ1) в земную систему координат (OXз, ОYз, OZз). А для этого на борту объекта понадобятся ещё дополнительные гироскопические приборы для определения УГЛОВОГО положения объекта (углы тангажа, рыскания и крена) относительно земной системы координат. Методика проектирование ускорений между связанной и земной системами координат в данной статье рассматривать не будем.
Затем, за счёт интегрирования УСКОРЕНИЙ, спроектированных в земную систему координат, получим сначала проекции СКОРОСТЕЙ движения относительно земной системы координат, а после интегрирования скоростей получим и ДЕКАРТОВЫЕ КООРДИНАТЫ объекта в земной с.к., т.е. его полную траекторию.
Кстати, по вертикальной оси земной системы координат OYз надо добавить ускорение свободного падения g(h) со знаком минус (см.ниже выр. 6.7), к измеренному акселерометром «кажущемуся» вертикальному ускорению поскольку, как уже неоднократно отмечалось, он не способен измерять ускорение от воздействия гравитации Земли на движение летательного аппарата. Это и понятно, т.к. например, в горизонтальном полёте акселерометр измерит вертикальное ускорение от подъёмной силы корпуса, равной численно силе притяжения аппарата к земле. Вычтя из этого измеренного ускорения акселерометра, называемого «кажущимся», и численно равного g , вышеупомянутую поправку в виде (– g) , получим в сумме НУЛЕВОЕ вертикальное ускорение, а, следовательно, и нулевую вертикальную скорость в режиме горизонтального полёта, что полностью соответствует горизонтальному полёту летательного аппарата.
P.S. Следующая публикация будет на тему вывода уравнений для скорости и ускорения тел для так называемого (в теоретической механике) "сложного движения" точки, позволяющих распространить методику расчёта динамики движения тела, применяемую в инерциальных системах с использованием законов Ньютона, на неинерциальные вращающихся системы и движущиеся в общем случае с линейным ускорением начала системы координат.
Георгий 01.03.2020г. 23ч55мин время Моск.
Как рассчитать сложное движение тела в неинерциальной системе отсчёта.
Оглавление:
1. Понятие об инерциальной и неинерциальной системах отсчёта (или системах координат).
2. Основные теоремы для системы рассматриваемых космических тел.
3. Сложное движение материальной точки. Теоремы о сложении скоростей и ускорений.
3.1 Основные определения. Абсолютная и относительная производные вектора.
3.2 Теорема о сложении скоростей для двух систем координат.
3.3 Теорема о сложении ускорений (теорема Кориолиса).
3.4 Применение основных теорем механики в неинерциальных системах отсчёт
Выбор системы отсчёта для расчёта траектории тела относительно неё представляется весьма важным начальным фактором, определяющим, в итоге, теоретически обоснованную надёжность расчётов траекторий космических тел. Рассмотрим подробнее вопрос выбора и размещения начала системы координат и проведём анализ всех возможных видов «кажущихся» ускорений, появляющихся в неинерциальных системах отсчёта вследствие их вращения и ускоренного перемещения начала системы отсчёта.
« ИНЕРЦИАЛЬНАЯ ситема отсчёта это такая система отсчёта, в которой справедлив закон движения по инерции свободной материальной точки, когда на неё не действуют никакие силы (или действуют взаимно уравновешенные силы) и при этом тело находится в состоянии покоя или равномерного прямолинейного движения по отношению к такой системе отсчёта.
Всякая система отсчёта, движущаяся по отношению к инерциальной поступательно, равномерно и прямолинейно, является также инерциальной. Следовательно, теоретически может существовать сколько угодно равноправных инерциальных систем, обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (так называемый «принцип относительности Галилея»). т.е. законы и уравнения механики не изменяются при: линейных сдвигах системы по осям координат, при угловых поворотах вокруг осей координат на некоторый угол, при «сдвиге по времени» (на dt) и при разных значениях равномерной поступательной скорости самой системы координат.
Помимо закона инерции, в любой инерциальной системе справедливы все три закона механики Ньютона, закон притяжения тел и законы сохранения количества движения (импульса), момента количества движения и движения центра инерции (или центра масс) для замкнутых, т. е. не подверженных внешним воздействиям, систем (см. подробнее первую статью данного цикла, посвящённую законам Ньютона и его Определениям I-VI).
Строго говоря, понятие об инерциальной системе является идеальной абстракцией. Реальная система отсчёта связывается всегда с каким-нибудь конкретным телом (Землёй, корпусом корабля или самолёта и т. п.), по отношению к которому и изучается движение тех или иных объектов. А поскольку в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звёздам и т. д.), то любая реальная система отсчёта может рассматриваться как инерциальная лишь с той или иной степенью приближения. С очень высокой степенью точности инерциальной системой можно считать Солнечную систему с началом в центре Солнца (точнее, в центре масс (центре инерции) Солнечной системы, т.е. в барической системе отсчёта) и с осями, направленным на далёкие звёзды. Такая инерциальная система используется в задачах небесной механики и космонавтики. Для решения большинства технических задач инерциальной системой практически может служить система, жёстко связанная с Землёй, а в случаях, требующих большей точности (напр., в гироскопии), - с началом в центре Земли и осями, направленными на звёзды.
Если система отсчёта движется по отношению к инерциальной системе с линейным ускорением и(или) вращается, то она является НЕИНЕРЦИАЛЬНОЙ СИСТЕМОЙ ОТСЧЁТА. При этом выражения всех вышеназванных законов, записанные в инерциальной системе требуют введения дополнительных членов, компенсирующих отличия в движении неинерциальной системы (её ускорения и вращения) от инерциальной.
Объясняется это тем, что ПО ОТНОШЕНИЮ К НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЁТА МАТЕРИАЛЬНАЯ ТОЧКА, находящаяся под воздействием реальных сил, (например, сил гравитационного притяжения между космическими телами) и не испытывающая воздействия никаких дополнительных реальных сил со стороны неинерциальной системы), ДОЛЖНА БЫТЬ ОСВОБОЖДЕНА НАМИ В ЕЁ ДИНАМИЧЕСИХ УРАВНЕНИЯХ ДВИЖЕНИЯ ОТНОСИТЕЛЬНО НЕИНЕРЦИАЛЬНОЙ СИТЕМЫ ОТ ФАКТИЧЕСКИ ПРИПИСЫВАЕМЫХ ЭТОМУ ТЕЛУ В ЭТОЙ СИСТЕМЕ «КАЖУЩИХСЯ» (МНИМЫХ И РЕАЛЬНО НЕ СУЩЕСТВУЮЩИХ) ДОПОЛНИТЕЛЬНЫХ УСКОРЕНИЙ, КОТОРЫЕ НЕ ВЫЗВАНЫ ДЕЙСТВИЯМИ НИКАКИХ РЕАЛЬНЫХ СИЛ, А ПОЯВЛЯЮЩИХСЯ ТОЛЬКО ИЗ-ЗА НАЛИЧИЯ «УСКОРИТЕЛЬНЫХ» ЭВОЛЮЦИЙ У САМОЙ НЕИНЕРЦИАЛЬНОЙ СИСТЕМЫ (относительно инерциальной системы), КОТОРЫЕ ОНА СО СВОЕЙ СТОРОНЫ (со своей, например, кружащейся вращающейся «больной головы» перекладывает на «здоровую» голову, т.е. на реально не вращающееся рассматриваемее нами тело, заставляя его также кружиться, как и она сама кружится при этом даже не подозревая ничего о собственном вращении, считая себя НЕ кружащейся!) ПРИПИСЫВАЕТ РАССМАТРИВАЕМОМУ НАМИ ТЕЛУ и которые вызваны следующими параметрами движения, присущими неинерциальной системе отсчёта:
1. ЛИНЕЙНЫМ УСКОРЕНИЕМ и НАЛИЧИЕМ при этом ЛИНЕЙНОЙ СКОРОСТИ начала неинерциальной системы,
2. ВРАЩЕНИЕМ ВОКРУГ НАЧАЛА СИСТЕМЫ ОТСЧЁТА (центростремительное ускорение вращения), а также и, возможно,
3. УСКОРЕННЫМ ВРАЩЕНИЕМ (угловое ускорение), и, наконец,
4. КОРИОЛИСОЫМ УСКОРЕНИЕМ, возникающим только при одновременном наличии линейной скорости перемещения тела относительно неинерциальной системы и угловой скорости вращения системы.
Примечание: Уважаемые читатели, кому не хочется тратить время (на чтение методики вывода ускорений в неинерциальных системах), могут сразу переходить к последнюю часть раздела 3.4 к выражениям (33) и (34) для ускорений в неинерциальной системе отсчёта.
2. Основные теоремы для системы рассматриваемых космических тел.
Давным-давно, в годы моей юности, в начале 60х годов, в школьном курсе физики А.В.Пёрышкина теоремы для систем тел не рассматривались, а преподавались в высшей школе в курсе «Теоретической механики». А вот в современных учебниках для 10 классов профильного и даже базовых уровней, в частности, двух разных учебниках под редакцией Г.Я.Мякишева, уже излагаются многие вопросы из курса теоретической механики такие, например, как закон сохранения импульса системы, о котором и пойдёт ниже речь как об основополагающем законе для выбора места расположения рациональной системы координат по расчёту космических траекторий.
Все теоретические формулы и большинство нижеследующих описаний взяты мной из понравившегося мне учебного пособия для студентов Московского Физтеха (МФТИ) (М.А. Айзерман «Классическая механика», Издание третье, Москва, Издательство Физико-математической литературы, 2005г, 380с.).
«Книга отличается систематически проведенным подходом, опирающимся на инвариантность и ковариантность законов и уравнений механики по отношению к преобразованиям систем отсчета», не встречавшемся ранее мне в обычных учебниках по «Теоретической механике» для студентов ВТУЗ-ов. Книга помогла взглянуть по новому на многие вопросы, связанные с рассмотрением инерциальных и неинерциальных систем отсчёта в механике. Поэтому большинство теоретических выражений и некоторых идей, изложенных ниже, позаимствовано из данной книги со ссылками на неё в соответствующих местах.
Количество движения системы материальных точек. (стр.72-74 книги)
Рассмотрим понятия о количестве движения системы тел, центре инерции системы, теорему об изменении количества движения системы (или теорему о движении центра системы) и сделаем вывод о постоянстве скорости движения центра инерции для замкнутой (не подверженной внешним воздействиям) системы тел в современном изложении.
Введём основные понятие о системе рассматриваемых тел (mi, где mi – масса тела с №=i, i=1,2…n; n-число тел в системе).
*) Далее во всех символах знака суммирования (Σ) подразумевается суммирование по i от 1 до n, т.е. по всем телам системы тел.
Количество движения сиcтемы тел есть вектор Q :
Q = Σ qi = Σ (mi · Vi); где жирным шрифтом обозначены векторные величины… (1)
Второй закон механики был сформулирован И. Ньютоном в труде «Начала…» в следующем виде:
«Производная по времени от количества движения системы равна главному вектору все действующих на систему внешних сил», а это и есть ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ ТЕЛ:
(dQ / dt) = Σ (mi· dVi / dt) = Σ (Fi) = Fвнешняя …………….……………………….. (2)
Центром инерции системы, для которой рассчитываются расстояния (ri) от начала исходной инерциальной системы координат до тел, является точка С, задаваемая радиусом-вектором rc :
rc = Σ (mi · ri) / Σ mi ; где: M = Σ mi называется МАССОЙ СИСТЕМЫ ТЕЛ ……….... (3)
Кстати, при воздействии однородного поля тяжести понятие ЦЕНТРА ИНЕРЦИИ СОВПАДАЕТ с понятием ЦЕНТРА ТЯЖЕСТИ материального ТЕЛА : rц.т. = Σ (Gi · ri) / Σ Gi ;
Дифференцирование по времени выр. (3) даёт позволяет найти выражении для ВЕКТОРА СКОРОСТИ ЦЕНТРА ИНЕРЦИИ СИСТЕМЫ:
Vc = Σ (mi · Vi) / Σ mi ; ……………………………………………………………. (4)
Из равенства (4) следует, что Q = Σ (mi · Vi) = M · Vc ; ……………..……………………. (5)
В итоге, количество движения системы тел равно произведению МАССЫ системы на СКОРОСТЬ ЕЁ ЦЕНТРА ИНЕРЦИИ.
Дифференцирование по времени выр. (5) позволяет выразить второй закон механики Ньютона для материальной точки, которая помещена в центре инерции системы и движется вместе с ним как точка с массой, равной массе системы тел M, к которой приложена равнодействующая всех внешних сил Fвнешняя:
(dQ / dt) = M · (dVc / dt) = Fвнешняя ………….……….…………..……………….. (6)
Выр. (6) следует новый вариант теоремы об изменении количества движения системы, называемый как ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА ИНЕРЦИИ СИСТЕМЫ ТОЧЕК :
«При движении системы материальных точек её центр инерции движется так, как двигалась бы материальная точка, помещённая в центре инерции системы, если бы в ней были сконцентрированы массы всех точек системы и к ней были бы приложены все внешние силы, действующие на все точки системы».
Введём понятие замкнутой системы точек, которая движется только под влиянием внутренних взаимодействий, т.е. взаимодействий материальных точек, входящих в систему. Это, конечно, условное понятие, т.к. в реальном мире все объекты взаимосвязаны гравитационными взаимодействиями в принципе при любых расстояниях между материальными объектами. Однако при идеализации задачи можно пренебречь относительно слабыми взаимодействиями других внешних объектов по сравнению с взаимодействиями точек, входящими в систему. Так, например, два небесных тела Землю и Луну, можно считать замкнутой системой, если интересует лишь взаимное движение между ними и пренебрегают воздействием на них остальных небесных тел, в том числе Солнца и других планет. Или, например, три небесных тела Солнце, Землю и Луну считают замкнутой системой, если учитывают лишь взаимодействие между этими телами и пренебрегают воздействием других планет Солнечной системы на их движение. Солнечная система в целом является примером замкнутой системы лишь в тех случаях, когда считают возможным пренебречь воздействием на тела Солнечной системы других внешних материальных объектов Вселенной. (стр.43)
У замкнутых систем, по их определению, Fвнешняя = 0, и тогда из выр.6 следует, что
(dVc / dt) = 0 ; а, следовательно и Vc = const; …………………………………… (7)
Поэтому закон сохранения количества движения можно сформулировать так:
«ЦЕНТР ИНЕРЦИИ ЗАМКНУТОЙ СИСТЕМЫ ДВИЖЕТСЯ С ПОСТОЯННОЙ СКОРОСТЬЮ (быть может и равной нулю)».
Можно сравнить эту теорему с её изложением у Ньютона в Следствии IV к 3-му Закону:
«Центр тяжести системы двух или нескольких тел от взаимодействия тел друг на друга не изменяет ни своего состояния покоя, ни движения; поэтому центр тяжести системы всех действующих друг на друга тел (при отсутствии внешних действий и препятствий) или находится в покое, или движется равномерно и прямолинейно.»
Разумеется, это утверждение верно и для проекций соответствующих векторов. Если проекция главного вектора внешних сил на некоторую ось тождественно равна нулю, то и центр инерции движется так, что проекция скорости центра инерции на эту ось остаётся постоянной.
Далее будет весьма удобно вводить в рассмотрение систему отсчёта, которая движется поступательно и начало которой помещено в центр инерции системы. Такую систему отсчёта будем называть далее ЦЕНТРАЛЬНОЙ. В том случае, когда скорость центра инерции системы точек ПОСТОЯННА, ЦЕНТРАЛЬНАЯ СИСТЕМА является ИНЕРЦИАЛЬНОЙ.
Из §3 Момент количества движения системы материальных точек (кинетический момент) (стр.74-76):
Выберем в нашей инерциальной системе произвольную точку А, которую назовём полюсом, и относительно которой определим момент от вектора количества движения каждой из материальных точек системы qi (= mi · Vi ) относительно этого полюса А с учётом вектора расстояния точки ri до полюса А в виде векторного произведения:
KАi = (ri × qi) = (ri × mi·Vi) …………………………….………………………… (8)
Вектор Ki называется моментом количества движения i-ой точки относительно полюса А. Символ «х» является символом ВЕКТОРНОГО произведения двух векторов.
*) Справка: Для определении положения и направления вектора Ki, являющегося результатом векторного произведения двух векторов ri и Vi в декартовой системе координат,
используется правило ПРАВОЙ руки (но не левой!), когда три пальца правой руки (большой, указательный и средний) распрямляем во взаимно перпендикулярные положения друг относительно друга (моделируя этим направления трёх осей декартовой системы координат), то при совмещении по направлению двух пальцев с первым (ri) и вторым векторами (Vi) из векторного произведения и при выполнении КРАТЧАЙШЕГО ПОВОРОТА от первого вектора ко второму (при взгляде на конец третьего пальца правой руки в сторону его основания) (этот кратчайший) ПОВОРОТ от первого вектора ко второму должен быть ВИДЕН ПРОТИВ ДВИЖЕНИЯ ЧАСОВОЙ СТРЕЛКИ. Тогда третий палец и будет отображать положение и направление итогового вектора (K), являющегося результатом векторного произведения двух исходных векторов (ri × mi·Vi) в выр.(8).
Главным моментом количества движения всей системы материальных точек будет их векторная сумма всех моментов материальных точек системы относительно полюса А, т.е. кинетическим моментом системы:
KА = Σ KАi = (ri × mi·Vi );
Если точку полюса А, используемую выше для расчёта кинетического момента, расположить в центре инерции системы, то получим, опуская вывод, ТЕОРЕМУ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА СИСТЕМЫ ТОЧЕК при воздействии на систему момента от внешних сил, приложенных к токам системы относительно центра инерции системы:
(dKА / dt) = M A внеш. ………………………………………………………… (9)
Производная от кинетического момента системы материальных точек (относительно неподвижного полюса А) равна главному моменту внешних сил, приложенных к точкам системы, относительно этого же полюса.
Для замкнутых систем выполняется условие M A внеш. = 0, т.к. на материальные точки ЗАКНУТОЙ системы (по определению) не действуют внешние силы и момент нечем создавать. Отсюда следует ЗАКОН СОХРАНЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА:
При движении ЗАМКНУТОЙ системы материальных точек её кинетический момент относительно любого неподвижного полюса НЕ МЕНЯЕТСЯ.
3. Сложное движение материальной точки. Теоремы о сложении скоростей и ускорений.
При написании данного весьма важного раздела взята за основу глава XIII «Сложное движение точки» (учебник для ВТУЗ-ов, Н.В.Бутенин, Я.Л.Лунц, Д.Р.Меркин «Курс классической механики» том I Статика и Кинематика, издание 4, Москва «НАУКА», 1985г, стр.203-208) как простое и типичное изложение для инженеров-механиков, смысл которого весьма прост и состоит во взятии сначала производной по времени от радиуса-вектора рассматриваемой точки, проведённого из начала неинерциальной системы отсчёта к рассматриваемой точке, для получения её вектора скорости, а затем во взятии производной по времени уже от вектора скорости точки для получения её вектора относительного ускорения в неинерциальной системе отсчёта.
3.1 Основные определения. Абсолютная и относительная производные вектора.
В этом разделе будет рассмотрен вывод выражения для первой производной от радиуса-вектора рассматриваемой точки по времени для получения выражения её вектора скорости и использованием правил дифференцирования векторов из курса линейной алгебры.
Рассмотрим движение одной и той же материальной точки М относительно двух систем: неподвижной инерциальной (назовём её: абсолютной) Системы Координат (СК) и неинерциальной (назовём её – подвижной СК) с центром в точке A , движущейся в самом общем виде с линейным ускорением начала системы координат и вращением относительно него с вектором угловой скорости ω.
Будем называть «АБСОЛЮТНЫМ» (или СЛОЖНЫМ) движением материальной точки М её движение относительно неподвижной инерциальной системы. Движение точки по отношению к подвижной системе назовём ОТНОСИТЕЛЬНЫМ. Под ПЕРЕНОСНЫМ движением будем понимать движение подвижной системы координат относительно неподвижной.
Зададим в подвижной СК расстояние от её начала до материальной точки М вектором расстояния r. Абсолютное движение точки М названо ещё и сложным потому, что ниже представим его ещё и как сумму двух движений: переносного движения самой подвижной системы координат относительно неподвижной системы и относительного движения точки М в подвижной системе. Поскольку нам понадобится операция дифференцирования по времени вектора расстояния r, определённого в подвижной системе координат, то введём понятие абсолютной и относительной производных.
Пусть задан вектор расстояния r(t) в подвижной СК, имеющий три проекции на оси подвижной СК: rx, ry, rz . Если ввести понятие трёх единичных векторов подвижной системы i, j, k,(их ещё называют ортами системы координат, в данном случае это орты подвижной СК) то вектор r может быть представлен в виде геометрической суммы трёх своих составляющих проекций на оси подвижной СК:
r (t) = rx i + ry j + rz k. *) ........................................................................................... (10)
*) знак скалярного умножения в виде точки (·), который должен стоять перед единичными векторами опущен для упрощения записи как в выр.(10), так и во всех нижеследующих выражениях.
Продифференцируем обе части равенства (10) по времени, имея в виду, что единичные вектора подвижной СК (i(t), j(t), k(t)) несмотря на свою постоянную длину, равную единице, из-за вращения СК также вращаются в пространстве и поэтому являются функцией времени и обладают тангенциальными линейными скоростями, приложенными к концам единичным векторов и перпендикулярными самим векторам, точно так же, как, например, вектор линейной скорости кругового вращения перпендикулярен вектору-радиусу вращающейся с постоянной скоростью точки и являются функцией времени. Напоминаем о правиле для взятия производной по времени от произведения двух функций U(t) и V(t), зависящих от времени, состоящем в том, что полная производная от произведения двух функций, зависящих от времени, равна произведению производной по времени от первой функции, умноженной на вторую функцию, плюс произведение первой функции на производную по времени от второй функции, т.е.:
(d(U V) / dt) = (dU/dt) V + U (dV/dt) ………………………………………………..(11)
что в применении дифференцирования по времени к выражению (10) после группировки членов даёт:
(dr/dt) = (drx/dt) i + (dry/dt) j + (drz /dt) k + rx (di/dt) + ry (dj/dt) + rz (dk/dt). ….(12)
Сумма первых трёх слагаемых представляет собой производную вектора r относительно подвижной СК. Если бы мы поставили своей задачей изучать изменение вектора r по отношению к подвижной СК, то мы учитывали бы при этом лишь изменения проекций вектора на оси этой системы координат, т.е. только сумму первых трёх слагаемых.
Действительно, собственное движение самой системы, в которой мы, например, оказались (например, на Землю) нас обычно не интересует, и мы, будучи помещены в начало любой системы отсчёта сами как бы и не вращаемся и не движемся, а лишь наблюдаем за вращениями и перемещениями окружающих тел относительно нас, т.е. относительно начала системы отсчёта, поскольку всё в мире относительно. При этом сама система отсчёта реально не «подозревает» о собственном вращении относительно какой-либо другой системы отсчёта (ведь она самодостаточна ) и её вращение мы можем наблюдаем лишь с позиций другой системе отсчёта, например, инерциальной. Но эти относительные рассуждения не должны нас отрывать от суровой действительности, и РАССМАТРИВАТЬ ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ДРУГИХ СИСТЕМ ОТСЧЁТА МЫ ОБЯЗАНЫ ТОЛЬКО С ПОЗИЦИЙ ИНЕРЦИАЛЬНЫХ СИСТЕМ ОТСЧЁТА, т.к. только для них были выведены все законы движения, открытые Ньютоном, и применение которых мы хотим распространить также и на неинерциальные системы отсчёта.
Назовём сумму первых трёх слагаемых в (12) ОТНОСИТЕЛЬНОЙ, ИЛИ ЛОКАЛЬНОЙ производной и обозначим её как (dr/dt)отн.:
(dr/dt)отн. = (drx/dt) i + (dry/dt) j + (drz /dt) k . ……….……………………………………..… (13)
Для преобразования трёх последних слагаемых в выр. (12) вспомним векторное выражение связи между линейной скоростью вращения любой точки твёрдого тела (V) и её вектором угловой скорости вращения (ω) и заданном векторе расстоянии до рассматриваемой точки вращающегося тела (r).
Из рассмотрения теории вращения твёрдого тела (с вектором угловой скорости вращения ω), имеющего одну неподвижную точку, известно выражение в виде векторного произведения для определения линейной скорости любой точки твердого тела, вызванной этим вращением (194 стр):
V = (ω × r). *) …………………………………………………..…………………… (14)
*) Примечание: Символами векторного произведения в данном комментарии являются круглые скобки для двух перемножаемых векторов, написанных жирным шрифтом, с символом векторного произведения между ними в виде знака умножения: «×» (см.выр.14).
Определим величину модуля вектора линейной скорости вращения | V | , раскрыв правило для векторного произведения (14):
| V | = | ω | | r | sin(φ) = | ω | rнорм. . ……………….………………….………………………… (15)
Где φ – угол вежду вектором угловой скорости ω, направленного по оси мгновенного вращения твёрдого тела, проходящей через неподвижную точку, относительно которой и вращается тело,
и направлением вектора расстояния r от неподвижной точки до рассматриваемой вращающейся произвольной точки тела, а rнорм. - это модуль расстояние (длина нормали) от точки тела до мгновенной оси вращения тела, т.е. это радиус вращения обычного вращения точки тела по кругу, плоскость которого перпендикулярна мгновенной оси вращения.
Подставив в выр. (14) вместо вектора полного расстояния до точки (r) последовательно единичные вектора подвижной СК i, j, k получим выражения для их производных по времени, не забывая, что длина этих единичных векторов постоянна и равна 1:
V = (ω × r ). … (14)
(di/dt) = (ω × i); (dj/dt) = (ω × j); (dk/dt) = (ω × k). ……………..…..….…….… (16)
Вышеприведенные производные есть тангенциальные скорости (т.е. перпендикулярные плоскостям, проходящем через вектор вращения СК ω и какую-либо из осей СК ) единичных векторов вращающейся СК.
Поэтому сумма последних трёх слагаемых из выр. (12) может быть преобразована к виду:
rx (di/dt) + ry (dj/dt) + rz (dk/dt) = rx (ω × i) + ry (ω × j) + rz (ω × k) =
= (ω × (rx i + ry j + rz k))= (ω × r); ….…….……… (17)
где ω – вектор угловой скорости подвижной системы координат. И, следовательно:
dr/dt = (dr/dt)отн. + (ω × r). ………… …………………………………………. (18)
где: (dr/dt)отн. = (drx/dt) i + (dry/dt) j + (drz /dt) k. … (13)
Таким образом, абсолютная производная по времени вектора в неподвижной системе координат равна сумме относительной производной этого же вектора в подвижной СК и добавочного вектора линейной скорости, вызванного вращением подвижной СК, и равного векторному произведению угловой скорости вращения подвижной СК на вектор расстояния до рассматриваемой материальной точки.
3.2 Теорема о сложении скоростей для двух систем координат.
Напомним, что мы рассматриваем движение одной и той же материальной точки М относительно двух систем: неподвижной (инерциальной СК) и подвижной (неинерциальной СК) с центром в точке А, движущейся в самом общем виде с линейным ускорением начала системы координат и вращением относительно него с вектором угловой скорости ω.
Найдём связь между следующими скоростями:
Абсолютной скоростью (V) материальной точки М относительно неподвижной инерциальной СК.
Относительной скоростью (Vr) по отношению к подвижной неинерциальной СК. Относительная скорость является движением относительно подвижной СК и по своей сути похожа на абсолютную скорость точки, являющуюся точно таким же движением, но по отношению к своей инерциальной СК.
А вот ПЕРЕНОСНАЯ скорость это нечто особенное из области «оптической иллюзии», когда собственное вращение и ускоренное перемещение начала подвижной СК целиком и полностью приписывается собственному движению точки М, поскольку само начало подвижной СК считает себя неподвижным и невращающимся центром, впрочем, как и все другие системы отсчёта, не исключая и инерциальные СК, это их коренное свойство, назовём манией собственного величия любой СК в виде её мирового центра - начала её системы координат («пупа»), вокруг которого всё и должно вертеться и двигаться, хотя с точки зрения другой, «трезвомыслящей» инерциальной СК, точка М переносную скорость (а в дальнейшем и разные виды вращательных ускорений) РЕАЛЬНО НА САМОМ ДЕЛЕ НЕ РАЗВИВАЕТ.
В итоге, переносной скоростью (Ve) материальной точки М, является скорость точки подвижной СК которая в данный момент совпадает с точкой М и именно скорость этой совпавшей точки подвижной СК и приписывается точке М (без всякого наложения на неё какой-либо физической связи со стороны самой подвижной СК), но фиктивно и чисто внешне приписываемая точке М за счёт простого оптического слежения за ней из начала неинерциальной СК.
Пусть заданы два радиус-вектора расстояний: первый от начала неподвижной СК до рассматриваемой нами материальной точки R(t) и от начала неподвижной СК до начала подвижной СК RА(t) и замыкает этот треугольник векторов радиус-вектор r(t), который определяет положение точки М в подвижной СК, т.е.
R = RA + r ……………………..….………………………………………………. (19)
Для выяснения связи между векторами скоростей продифференцируем по времени треугольник векторов расстояний (выр.19):
V = (dR /dt) = (dRA /dt) + (dr /dt) = VA + (dr /dt). .……………….……….…. (20)
где: (dr/dt) = (dr/dt)отн. + (ω × r) . см.(18)
Немного ранее была специально для этого вычислена производная для радиус-вектора dr/dt (см. выр.18). Очевидно и то, что производная по времени от радиус-вектора начала подвижной СК (dRA/dt) равна вектору скорости начала подвижной СК, т.е. VA , а производная от радиус-вектора дальности точки М в подвижной СК – (dr/dt) отн. есть ни что иное, как вектор относительной cкорости Vr точки М в подвижной СК. Подставим всё это в выр.20:
V =VA + (ω × r) + (dr/dt)отн.;
V= (VA+(ω × r)) +Vr. - Абсолютная скорость как сумма переносной и относительной скоростей .(21)
Вектор абсолютной скорости равен векторной сумме переносной и относительной скоростей:
V = Ve + Vr; где: V - абсолютная скорость …………………………………….…… (22)
где: Ve = VA + (ω × r); - переносная скорость ………...……………....…………... (23)
Vr = (dr/dt) отн. = (drx/dt) i + (dry/dt) j + (drz /dt) k. - относительная скорость .... (24)
В итоге, получили формулировку для теоремы о сложении скоростей:
Абсолютная скорость точки относительно неподвижной СК равна геометрической сумме векторов переносной и относительной скоростей.
Выр.22 применяют для определения скорости космического тела в моменты перехода на границе «сферы переключения межпланетных траекторий» для нахождения начального значения вектора как относительной скорости при ВХОДЕ в «сферу» из неподвижной, например, Солнечной СК в СК какой-либо планеты по выр 25, вытекающему из выр. 22:
Vr = V – Ve, …..…....……………………………………………………………. (25)
где: Ve = VA + (ω × r) – переносная скорость, а VA - орбитальная скорость планеты относительно Солнца, ω – угловая скорость собственного вращения планетной СК (если применена инерциальная, не вращающаяся планетная СК, то ω = 0 и Ve =VA), а радиус-вектор r равен радиусу «сферы переключения межпланетных траекторий». При выходе из «сферы» для определения начального значения скорости тела в Солнечной СК применяют выр.22.
В итоге, выр.23 для ПЕРЕНОСНОЙ СКОРОСТИ (Ve), вызванная скоростными эволюциями начала подвижной СК, ПРИПИСЫВАЕТ материальной точке М, НЕСУЩЕСТВУЮЩУЮ РЕАЛЬНО, «ФИКТИВНУЮ» и ИЛЛЮЗОРНУЮ СКОРОСТЬ (относительно начала подвижной СК), не вызванную НИКАКИМИ ФИЗИЧЕСКИМИ ВОЗДЕЙСТВИЯМИ на материальную точку М, а объяснимую лишь эффектом визуального перемещения точки М относительно начала подвижной СК.
Например, можно запросто «разогнать» относительную скорость тела М в подвижной СК, не прикладывая никаких реальных сил к материальному телу, до околосветовых скоростей при умеренной угловой скорости вращения ω лишь самой подвижной СК. Это напоминает опыт Майкельсона по определению скорости света, где в качестве подвижной СК выступает легкая, быстро вращающаяся СК в виде платформы с закреплённой на ней зеркальной призмой, отражающей луч света. Ну и как тут не назвать все эти кажущиеся, нереальные скорости, возникающие в подвижной вращающейся СК из-за её собственного вращения, не иначе как МНИМЫМИ И «ФИКТИВНЫМИ», а вот такие же «фиктивные» иллюзорные ускорения и, соответствующие им разные виды «сил инерции», рассмотрим в следующем разделе.
Вот что написал в своих «Началах…» И.Ньютон по этому поводу:
«Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения. Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется.»
*) Примечание: Добавим, что, так термин «относительное движение» у Ньютона в инерциальной системе на современном языке соответствует понятию «переносное движение» в неинерциальной системе, которое можно создать вообще без всяких сил, сообщив вращение или линейную скорость началу неинерциальной системы координат.
3.3 Теорема о сложении ускорений (теорема Кориолиса).
Для нахождения абсолютного ускорения точки по отношению к инерциальной системе координат продифференцируем по времени выр.21 теоремы сложения скоростей для абсолютной скорости:
V = (VA + (ω × r)) + Vr;
где: Vr = (dr/dt) отн. = (drx/dt) i + (dry/dt) j + (drz /dt) k. – относительная скорость …(21)
W = (dV/dt) = (dVA/dt) + [ ((dω/dt) × r) + (ω × (dr/dt)) ] + (dVr/dt). ………………… (26)
где: ранее было выведено выр. : dr/dt = (dr/dt)отн. + (ω × r). …….(18)
Абсолютную производную для вектора относительной скорости Vr найдём по универсальной формуле (18) для взятия производной от векторов в двух системах: неподвижной и подвижной
(dVr/dt) = (dVr/dt)отн. + (ω × Vr) . ……….……………………………………. (27)
В этом выражении (dVr / dt)отн. есть относительная производная вектора Vr по времени и, следовательно, представляет собой относительное ускорение Wr, т.е. ускорение точки по отношению к подвижной СК:
Wr = (dVr/dt)отн. = (d2rx/dt2) i + (d2ry/dt2) j + (d2rz/dt2) k. - относительное ускорение …(28)
Используя подстановку равенств (18), (13), (25) и (26) в формулу (24) преобразуем её:
W = WA + ((dω/dt) × r) + (ω × (Vr + (ω × r)) ) + Wr + (ω × Vr) .
W = WA + ((dω/dt) × r) + (ω × (ω × r)) + Wr + (2ω × Vr), ……………...…… (29)
где: WA = (dVА /dt) и (dω/dt) линейное и угловое ускорения начала подвижной СК.
Для того, чтобы выделить только переносное ускорение We для материальной точки М, которое ей приписывается наблюдателем жёстко зафиксированным к началу подвижной СК вращающимся вместе с подвижной СК, отслеживать ПЕРЕНОСНОЕ движение подвижной СК, т.е. перемещение точки М относительно подвижной СК (ускорение той точки, жёстко закреплённой относительно осей подвижной СК, с которой в данный момент ТОЛЬКО совпадает СВОБОДНАЯ И НИКАК НЕ СВЯЗАННАЯ с подвижной СК движущаяся материальная точка, сложное движение которой мы и пытаемся определить), закрепим точку в подвижной СК, т.е. положим Vr = 0 и Wr = 0. В этом случае из выр.(27) будем иметь выр. для переносного ускорения We, которое испытывает точка ЖЁСТКО ЗАФИКСИРОВАННАЯ относительно подвижной СК, т.е. представляющая единое твёрдое тело вместе с осями подвижной системы координат:
We = WA + ((dω/dt) × r) + (ω × (ω × r)). – Это переносное ускорение ……………. (30)
Итак, это и есть переносное ускорение точки свободного твёрдого тела, с которым жёстко связана подвижная СК и которая в данный момент совпадает с рассматриваемой нами материальной точкой М, и которой формально приписываются все эти «иллюзорные» ускорения. Переносное ускорение представляет собой сумму линейного ускорения начала подвижной СК ( WA ) с вектором (dω/dt × r), называемого ВРАЩАТЕЛЬНЫМ УСКОРЕНИЕМ. При вращении вокруг неподвижной оси направления векторов (dω/dt) и ω всегда совпадают и поэтому вектора скорости и касательного ускорения направлены вдоль одной и той же прямой по касательной траектории. Последний дополнительный вектор в переносном ускорении (ω × (ω × r)) называют осесимметричным ускорением.
По аналогии с анализом выр. (14) ( V = (ω × r ) ) в виде выр.(15) для модуля скорости вращающееся точки ( | V | = | ω | | r | sin(φ) = | ω | rнорм. ) можно показать, что модуль вектора
| ω × ( ω × r )| = | ω | 2 | r | sin(φ) = | ω |2 rнорм. в отличие от модуля скорости (во вращательном движении по кругу, плоскость которого перпендикулярна мгновенной оси вращения) направлен не по касательной к кругу вращения с радиусом вращения rнорм, а по нормали к траектории вращения вокруг мгновенной оси , т.е. вдоль вектора rнорм и направлен к оси мгновенного вращения, как бывает обычно направлен вектор центростремительного ускорения при вращении по кругу с радиусом rнорм. Это и есть осесимметричное ускорение, увлекающее точки твёрдого тела во вращательное движение вокруг мгновенной оси вращения. Естественно оно и породит в подвижной системе противоположно ему направленное всем известное ЦЕНТРОБЕЖНОЕ УСКОРЕНИЕ.
В итоге, имеем выражение для полного ускорения материальной точки:
W = We + Wr + (2ω × Vr) . …..……………………………………….……. (31)
Ускорение, определяемое членом (2ω × Vr), называется поворотным или кориолисовым ускорением, т.е. кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости перносного движения на скорость точки в её относительном движении:
Итак, имеем
W = We + Wr + Wc. -Абсолютное (полное) ускорение относительно неподвижной СК …... (33)
где: Wr = (dVr/dt)отн.=(d2rx/dt2) i + (d2ry/dt2) j + (d2rz/dt2) k. -Относительное ускорение(28)
We = WA + ((dω/dt) × r) + (ω × (ω × r)). –Переносное ускорение(30)
Wс = (2ω × Vr). - Кориолисово ускорение ……..………………… .………………..(34)
Это и есть содержание теоремы Кориолиса: Абсолютное ускорение точки можно рассматривать как геометрическую сумму переносного, относительного и кориолисова ускорений за счёт введения в рассмотрение подвижной СК, начало которой обладает линейной переносной скоростью ( VA ) и ускорением ( WA ), а также вращается с угловой скоростью (ω), имеющей в общем виде и угловое ускорении( dω/dt ) и при наличии скорости перемещения рассматриваемой точки относительного подвижной СК (Vr). Направление кориолисова ускорения определяется как и для всех векторных произведения в помощью правила правой руки, описанного в начале статьи (см. справку под выр.(8).
3.4 Применение основных теорем механики в неинерциальных системах отсчёта
(Данный раздел написан по материалам §8.гл.3 книги «Классическая механика» М.А.Айзерман.стр.106-110).
Рассмотрим движение материальной точки в неинерциальной системы в сравнении с её же движением относительно инерциальной системы. Наблюдатель, находящийся в инерциальной СК, имеет право для изучения динамики движения тоски применять законы механики и в частности второй закон Ньютона:
mi Wi = Fi. ………………………………………………………………………. (35)
где Wi – проекции ускорения точки относительно инерциальной системы на её оси x,y,z.
Попытка применить второй закон в неинерциальной системе приведёт к тому, что закон Ньютона не будет выполняться, т.к. умножение массы точки на ускорение, которое наблюдается в неинерциальной системе, приведёт к получению силы отличающейся от реально действующей на точку силы в законе (35). Разница вызвана появлением дополнительных ускорений в неинерциальной системе (см.выр. 33,28,30 и34), вызванных неинерциальностью системы: вращением осей системы координат с угловой скоростью (ω) и наличием линейного ускорения у начала сиcтему координат (WA). Движение точки mi можно считать сложным движением:
Движение точки mi относительно инерциальной системы можно рассматривать как АБСОЛЮТНОЕ, движение точки mi относительно неинерциальной системы – как ОТНОСИТЕЛЬНОЕ, а движение неинерциальной системы относительно инерциальной системы отсчёта – как ПЕРЕНОСНОЕ. Тогда в соответствии с выр.33:
W (абс) = We (пер) + Wr (отн.) + Wc (кор.) ………………………………………………… (36)
В качестве ускорения в левой части выр.36 фигурирует ускорение точки mi относительно инерциальной системы, т.е. как раз то ускорение, которое теперь, рассматривая движение точки mi как сложное, мы назвали АБСОЛЮТНЫМ, подставляя выр.36 во второй закон Ньютона (выр.35), получаем:
mi (We (пер) + Wr (отн.) + Wc (кор.)) = Fi.
Перепишем это соотношение для определения ОТНОСИТЕЛЬНОГО ускорения, что позволит записать второй закон Ньютона применительно к НЕИНЕРЦИАЛЬНОЙ системе отсчёта:
mi Wr (отн.) = Fi - mi We (пер.) - mi Wc (кор.) ………………………………………… (37)
*) Примечание: Для инженерного применения больше подходит вариант выр. 37 БЕЗ ПЕРЕХОДА к инерционным силам, а сразу в ускорениях для каждого из рассматриваемого i-го тела системы тел:
Wri (отн.) = Fi / mi - Wei (пер.) - Wci (кор.) ……………………………………..……… (38)
Формулу (37) можно трактовать как запись второго закона Ньютона применительно к НЕИНЕРЦИАЛЬНОЙ системе отсчёта. В правой части появляются два новых члена в виде двух «сил» переносной (Ji пер) и кориолисовой (Ji кор), поскольку имеют размерность силы как произведение массы тела на ускорение, и в итоге получаем:
mi Wr (отн.) = Fi + Ji пер. + Ji кор. ……………….……………………………………..… (39)
где: Ji пер. = - mi We (пер.), Ji кор. = - mi Wc (кор.) ……….. (40)
Новые два вектора в правой части формулы (38) имеют размерность силы и называются СИЛАМИ ИНЕРЦИИ: вектор Ji пер. называется ПЕРЕНОСНОЙ силой инерции, а вектор Ji кор. – КОРИЛИСОВОЙ силой инерции. Обратите внимание, что НАПРАВЛЕНИЕ сил инерции ПРОТИВОПОЛОЖНО направлению соответствующих ускорений!
Таким образом, мы установили, что второй закон Ньютона может быть применён и в неинерциальных системах отсчёта, если к силам, действующим на каждую точку , добавить переносную и кориолисову силы инерции!
Если все силы делятся на внешние и внутренние, то СИЛЫ ИНЕРЦИИ ОТНОСЯТСЯ К ВНЕШНИМ СИЛАМ. Так, например, теорему об изменении количества движения и теорему об изменении кинетического момента, можно записать так:
(dQ/dt) = Fвнешняя + Ji пер. + Ji кор. ……………….…………………………………………….… (41)
(dKА/dt) = MA внеш. + MA Jпер + MA Jкор. ……………………………………………….…. (42)
Для нас представляет особый интерес ЦЕНТРАЛЬНАЯ СИСТЕМА ОТСЧЁТА, расположенная в центре масс системы тел и которая движется поступательно относительно инерциальной системы так, что в любой момент времени скорость (ускорение) всех её точек СОВПАДАЕТ со скоростью (ускорением) ЦЕНТРА ИНЕРЦИИ рассматриваемой системы материальных точек. В центральной системе КОРИОЛИСОВЫХ сил НЕТ ( так как переносное движение ПОСТУПАТЕЛЬНО и ω = 0) и для связанного с ней наблюдателя центр инерции рассматриваемой системы материальных точек НЕПОДВИЖЕН (Vc = Wc = 0). Поэтому для такого наблюдателя из формулы Q = M (dVc/dt) = 0 всегда (т.е. не только для замкнутых систем, но и при любых внешних силах!): количество движения системы СОХРАНЯЕТСЯ равным нулю во время движения. Из теоремы о движении центра инерции:
M (dVc/dt) = R = Rвнешн. + Jпер. = 0.
следует, что в центральной системе главный вектор все сил, приложенных к точкам системы (включая силы инерции) равен нулю.
Георгий 04.02.2020г 23ч 50мин. Время моск.
P.S. В следующей теме будут проанализированы все виды ускорений, появляющихся в неинерциальных системах отсчёта в теореме Кориолиса с акцентом на анализ кориолисова ускорения, вызывающего интересные дискуссии о «правильности» выражения для него, поскольку многих смущает множитель 2 в выражении для кориолисова ускорения (2ω × Vr) особенно в случае, когда вектор относительной скорости Vr направлен тангенциально, т.е перпендикулярно радиусу-вектору рассматриваемой точки и его ускорение совпадает по направлению и накладывается на центростремительное ускорение, вызываемое обычным вращением точки, относительно начала подвижной системы координат с угловой скоростью систем ω, но кориолисово ускорение при этом превышает по своей величине в 2 раза обычное центростремительное вращательное ускорение.
К вопросу о переносном и кориолисовом ускорениях в неинерциальных системах отсчёта.
Предыдущий комментарий был посвящён выводу выражений для переносной скорости и всех видов ускорений, присущих неинерциальным системам отсчёта. В данном комментарии проанализируем все виды возможных ускорений в неинерциальных системах.
Но для начала проведём анализ окончательных выражения для всех возможных видов ускорений, которые возникают при расчёте движения материальной точки относительно подвижной неинерциальной системы отсчёта и которую для простоты понятия, назовём подвижной, в отличие от инерциальной неподвижной системы, которую так и назовём: неподвижной.
Вот они все выражения для всех возможных ускорений в подвижной системе перед нами:
W=We + Wr + Wc. - Абсолютное ускорение свободного тела в инерциальной системе отсчёта... (1)
где:
Wr =(dVr/dt)отн.=(d2rx/dt2) i + (d2ry/dt2) j + (d2rz/dt2) k. – Относительное ускорение свободного тела относительно неинерциальной вращающейся системы ………... (2)
We = WA + ((dω/dt) × r) + (ω × (ω × r)). – Переносное ускорение (реальное ускорение точек условного твёрдого вращающегося тела вместе с осями подвижной системы)….... (3)
Wс = (2ω × Vr). - Кориолисово ускорение (реальное ускорение подвижного тела, передвигающегося относительно вращающегося тела и имеющего с ним физическую связь)…. (4)
Выр.(1) - это и есть содержание теоремы Кориолиса: Абсолютное ускорение точки можно рассматривать в сложном движении как геометрическую сумму относительного, переносного и кориолисова ускорений за счёт введения в рассмотрение подвижной СК, начало которой может обладать в общем случае линейной переносной скоростью ( VA ) и ускорением ( WA ), а также может и вращаться с угловой скоростью (ω), обладающей в общем виде и угловым ускорением ( dω/dt ), возможно и наличие скорости относительного перемещения рассматриваемой нами точки относительно подвижной системы с линейной скоростью (Vr).
Для того, чтобы подвижная система отсчёта превратилась в НЕИНЕРЦИАЛЬНУЮ систему вполне достаточно либо наличия линейного ускорения у начала системы (WA), либо наличия у подвижной системы вращения угловой скорости вращения ω относительно инерциальной системы.
Важное замечание: Все выражения для ускорений(1-4), да и скоростей, были получены при условии, что рассматривалось движение АБСОЛЮТНО твёрдого подвижного тела с «закреплёнными» на нём, связанными осями подвижной системы. В учебниках по теоретической механике в начале подробно рассматривается вращение твёрдого тела с неподвижной точкой вращения, а затем и с подвижной, т.е. в общем виде движения вращающегося твёрдого тела. При этом уравнения для скоростей и ускорений точек тела получаются совершенно аналогичными вышеприведенным для подвижной системы отсчёта(1-3) с той лишь разницей, что при неподвижной точке вращения нет скорости и ускорения в этой точке, т.е. VA и WA, равны нулю, а вот при освобождении тела от неподвижной точки они появляются, да и ещё в этих уравнениях, естественно, так же нет кориолисова ускорения (Wс=0), поскольку тело жёсткое и нет никакого относительного перемещения (Vr=0) какого-либо материального тела относительно поверхности вращающегося условного твёрдого тела.
Так что, в итоге, все ускорения в выр.1-4 для подвижной неинерциальной системы отсчёта ВЫВЕДЕНЫ ТОЧНО ТАК ЖЕ, КАК И ДЛЯ ТОЧЕК ТВЁРДОГО ВРАЩАЮЩЕГОСЯ И ПЕРЕМЕЩАЮЩЕГОСЯ В ПРОСТРАНСТВЕ ЖЁСТКОГО ТЕЛА с учетом того факта, что относительная скорость (Vr) и ускорение (Wr) могут изменяться (в сравнении с уравнениями для твёрдого тела) за счёт, например, появления определённой физической связи, удерживающей некое подвижное тело в контакте с поверхностью вращающегося и в то же позволяющей ему свободу относительного перемещения со скоростью Vr по его поверхности, и поэтому все выр.1-4 являются действительными и реальными ускорениями как для любой точки твёрдого вращающегося тела, так и для некоего тела, перемещающегося со своей относительной скоростью Vr по его поверхности.
После подстановки выражения для ускорения движения тела из второго закона для тела, движущегося под воздействием равнодействующей всех сил в абсолютной системе ( W = F/m) в левую часть выр.1 и выделения в левую часть выражения, для искомого нами ускорения тела относительно подвижной системы (Wr) получим окончательное выражение
Wr = F/m –We –Wc = F/m + Wантипер. + Wантикор.; - Ускорение (относительное) свободного тела в неинерциальной системе.……. (5)
где:
Wr = (dVr/dt)отн. = (d2rx/dt2) i + (d2ry/dt2) j + (d2rz/dt2) k. - Относительное ускорение свободного тела в неинерциальной системе
We =WA + ((dω/dt) × r) + (ω × (ω × r)). - Переносное ускорение точек условного твёрдого вращающегося тела..(3)
Wантипер. = –We. - фиктивное (мнимое) «антипереносное» ускорение, приписываемое свободному телу...... (6)
Wс = (2ω × Vr). - Реальное кориолисово ускорение перемещающегося подвижного тела по поверхности вращающегося твёрдого тела и имеющему физическую связь с поверхнотью... (4)
Wантикор. = –Wc. - фиктивное (мнимое) «антикориолисово» ускорение, приписываемое свободному телу..... (7)
И где фиктивные (мнимые) ускорения (Wантипер. = –We) и (Wантикор. = -Wc) , стоящие в правой части выр.(5) можно назвать «антипереносным» и «антикориолисовым» ускорениями с учётом их фиктивности и противоположной направленности фактическим ускорениям точек условного твёрдого тела, вращающегося вместе с осями подвижной неинерциальной системы.
Ниже, для сравнения, приведены похожие выражения из учебника (М.А. Айзерман «Классическая механика» с стр.107 (см.выр.(8)и (9)):
mi Wr (отн.) = Fi + Ji пер. + Ji кор. ……………….……………………………….………..…... (8)
где: Ji пер. = – mi We (пер.), Ji кор. = – mi Wc (кор.) ……......………………. (9)
Обратите, пожалуйста, внимание на ВАЖНОЕ ОТЛИЧИЕ выражений (5-7) от выр. (8-9).
Моя ПРИНЦИПИАЛЬНАЯ ПОЗИЦИЯ ЗАКЛЮЧАЕТСЯ В ТОМ, ЧТО НЕ СТОИТ ВВОДИТЬ ПОНЯТИЙ ДЛЯ ФИКТИВНЫХ (МНИМЫХ и НЕСУЩЕСТВУЮЩИХ) «СИЛ ИНЕРЦИИ» и «СИЛЫ КОРИОЛИСА ИНЕРЦИИ» (в виде выражения (9)), А ВПОЛНЕ ДОСТАТОЧНО ОГРАНИЧИТЬСЯ ФИКТИВНЫМИ УСКОРЕНИЯМИ ВМЕСТО НИХ (–We) и (-Wc) (выр. (5-7), придав им единообразные названия с приставкой «АНТИ», т.е. противоположно направленные с предлагаемыми для них следующими названиями: «антипереносное» и «антикориолисово» ускорения.
*) Примечание: АНТИ (греч. Anti) - против, направленности против кого или чего-нибудь, приставка, употребляемая с другими словами для обозначения противоположности или противодействия.
При этом, получается, что приставка «АНТИ» носит УСИЛЕННЫЙ ДВОЙНОЙ смысл:
во-первых как противоположно направленное ускорение, о чём говорит знак МИНУС перед ускорением, а во-вторых, что ещё важнее, - приставка "анти" подчёркивает ФИКТИВНОСТЬ этих ускорений для нашего мира, как, например, понятие из потустороннего для нас несуществующего мира, т.е. антимира, состоящего из антивещества, где всё наоборот и в котором сила вызывает ускорение не в направлении действия этой силы (a =F/m) как это д.б. по первому закону Ньютона, а в противоположном направлении, т.е. (a = - F/m).
В итоге реальным переносному и кориолисову ускорениям точек вращающегося жёсткого тела и подвижного перемещающегося по поверхности твёрдого тела, движущегося по нему (см.выр. 3 и 4) противопоставляются их отрицательные по знаку «антипереносное» и «антикориолисово» ускорения (выр.3-7) – ФИКТИВНЫЕ, МНИМЫЕ И НЕСУЩЕСТВУЮЩИЕ РЕАЛЬНО, но приписываемые визуально при совмещении точек вращающегося (условного) твёрдого тела при их совпадении в пространстве с рассматриваемой нами свободной точкой только за счёт собственных эволюций, т.е. перемещения и вращения, условного твёрдого тела и при этом никоим образом физически не связанных с движением свободного тела в пространстве.
Как известно, понятие этих ФИКТИВНЫХ СИЛ ИНЕРЦИИ было введено Д’Аламбером и Эйлером для удобства расчёта в статике вместо динамики движения тела, когда к телу приложена взаимно уравновешенная система сил из реальных и мнимых, полученных чисто формальным путём за счёт умножения массы тела на вышерассмотренные фиктивные «антипереносное» и «антикориолисово» ускорения (см. выр.8-9), в т.ч. и ЗАМЕНЕ РЕАЛЬНОГО УСКОРЕНИЯ ТЕЛА (см. (F/m) в выр.(5) ), получаемого по второму закону в инерциальной системе, в ЕЩЁ одну фикцию в виде разновидности «МНИМОЙ СИЛЫ ИНЕРЦИИ», разменивающей ускоренное движение тела на эту самую «НЕЧИСТУЮ» СИЛУ, останавливающую его ускоренное движение и «замораживающее» тело в положение статичного равновесия под воздействием всего этого полностью уравновешенного букета разношёрстных сил.
Это всё и привело, в итоге, к этакому симбиозу в основном из МНИМЫХ И ФИКТИВНЫХ СИЛ СО ЗНАКАМИ МИНУС, в котором немудрено было многим заблудиться и принять их ЗА ВПОЛНЕ ОБЫЧНЫЕ реальные силы, под действием которых, можно якобы осуществлять перемещения тел, как например, это часто ошибочно думают о центробежной силе, считая её активной и самостоятельной.
Но ЦЕНТРОБЕЖНАЯ СИЛА эта ПО СУТИ ФИКТИВНАЯ, ВТОРИЧНАЯ, ОТВЕТНАЯ СИЛА РЕАКЦИИ, т.е. несуществующая и несамостоятельная по происхождению (в отличие от реальной активной центростремительной силы. За фальшивым фасадом центробежной силы и её ускорения стоит реальное проявление ИНЕРЦИОННОГО СВОЙСТВА ТЕЛА К СОХРАНЕНИЮ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ, от которого это тело УВОДЯТ В СТОРОНУ ЦЕНТРОСТРЕМИТЕЛЬНЫМ УСКОРЕНИЕМ, преодолевающим это ИНЕРЦИОННОЕ СВОЙСТВО МАССЫ ТЕЛА СОПРОТИВЛЯТЬСЯ ЭТОМУ ОТКЛОНЕНИЮ ОТ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ и реально сообщающему телу эллиптическую траекторию движения (по отношению к инерциальной системе), а по отношению к неинерциальной вращающейся системе сводящейся к взаимно уравновешенным векторам реального центростремительного ускорения и фиктивного «антиценростремительного» (т.е. центробежного) или тот же баланс в виде сил: центростремительной и «антицентростремительной» (т.е. центробежной) как сейчас повсеместно принято это преподносить.
Если реализовать предложенную выше СИСТЕМУ ТОЛЬКО ИЗ ФИКТИВНЫХ МНИМЫХ УСКОРЕНИЙ С ОБЯЗАТЕЛЬНОЙ ПРИСТАВКОЙ К НИМ «АНТИ», т.е. УСКОРЕНИЙ СО ЗНАКОМ МИНУС, И ОДНОВРЕМЕННО ОТКАЗАТЬСЯ ОТ РАССМОТРЕНИЯ СООТВЕТСТВУЮЩИХ ИМ ФИКТИВНЫХ СИЛ (СО ЗНАКОМ МИНУС ПЕРЕД ИХ ЖЕ «РОДНЫМ» УСКОРЕНИЕМ), то и не было бы никогда проблем с этой приснопамятной ФИКТИВНОЙ ЦЕНТРОБЕЖНОЙ СИЛОЙ, КОТОРОЙ БЫ ПРОСТО НЕ СУЩЕСТВОВАЛО ПО ОПРЕДЕЛЕНИЮ, а вместо неё фигурировало бы в уравнении второго закона движения только фиктивное «антицентростремительное» (ныне центробежное) ускорение. Также пропали бы из выражений динамики движения тела ВСЕ НЕСУЩЕСТВУЮЩИЕ МНИМЫЕ "СИЛЫ ИНЕРЦИИ", место которых в уравнениях движения заняли бы соответствующие им фиктивные ускорения со знаком минус. А главное, пропал бы и сам предмет спора о реальности "СИЛ ИНЕРЦИИ" по причине их ПОЛНОГО ОТСУТСТВИЯ в предлагаемой автором системе ускорений и сил.
Действительно, Д’Аламбер и Лагранж вполне могли бы обойтись применением СТАТИКИ ДЛЯ ВЕКТОРОВ УСКОРЕНИЙ ВМЕСТО СТАТИКИ СИЛ, никакой, в принципе, разницы, те же самые вектора, но промасштабированные по модулю (свое длине) умножением на обратную величину массы тела. Однако всех, видимо, попутала «нечистая сила», иначе говоря, так увлекла своим обаянием «СИЛА» (пускай и фиктивная, мнимая и несуществующая, но СИЛА). Как, например, и в современной рекламе на ТВ про Силу Сибири, Силу Красоты и т.п. букет Сил. И даже Ньютон не устоял, применив термин сила инерции, вместо свойства инерции массы, хотя в его законах и определениях нет никакого места фиктивным силам инерции, кроме как реальной «врождённой силы материи» в Определении III, которое не лишне будет повторить в данном месте:
« Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения.»
*) Хотя из самого текста Определения чётко видно, что Ньютон понимает под термином"врождённая сила материи" только "присущую ей СПОСОБНОСТЬ сопротивления", а это и есть скалярная селичина, а не векторная.
В итоге, давно пора навести порядок в терминологии теоретическтой механики в части наименований сил и ускорений, закрепить статус РЕАЛЬНЫХ НЬЮТНОВЫХ СИЛ за всеми реальными силами в механике, исключив все фиктивные "силы инерции" и оставив мнимый мир только ФИКТИВНЫМ УСКОРЕНИЯМ с приставкой «АНТИ» (и с присущим им знаком минус) для очищения и оздоровления физической реальности нашего мира. Да сгинут все мнимые «СИЛЫ ИНЕРЦИИ», оставив взамен себя лишь фиктивные мнимые отрицательные ускорения в уравнениях Ньютона для неинерциальных систем отсчёта.
Однако, после этой небольшой разборки с фиктивными "силами инерции", обратимся к подробному рассмотрению всех ускорений, возникающих в неинерциальных вращающихся системах.
1. Об относительном ускорении.
Относительное ускорение Wr (см.выр.(3)) рассматриваемой нами точки, как и её относительная скороcть Vr по своей сути является такими же параметрами относительного движения по отношению к своей подвижной (неинерциальной) СК, как и абсолютное ускорение (и абсолютная скорость) являются относительным движением по отношению к своей инерциальной СК и представляют собой простые вторые и первые производные по времени от радиусов-векторов расстояний точки до начала в двух систем отсчёта, включающие в себя только по три векторных составляющих, спроектированных на единичные орты в своих соответствующих системах отсчёта. Именно это относительное ускорение (и относительную скорость) для рассматриваемой нами точки, свободной от физических связей с подвижной системой отсчёта, мы и реально освободим от соседства с остальными ускорениями (переносным и кориолисовым) для того, чтобы получить «освобождённые» относительные ускорения для нашей свободной точки от, теперь уже ставших для её относительного движения «фиктивными» ускорениями, незаслуженно приписываемыми свободному телу от реальных ускорений точек условного жёсткого подвижного тела, которые совпадают по очереди в пространстве в каждый из моментов времени с нашей свободной точкой, но которые это свободное тело НЕ СОВЕРШАЕТ по причине своей свободы от связей с подвижной системой, что в итоге и обеспечит нам получение правильного результата расчёта движения точки при применении всех законов движения, справедливых и в инерциальных системах отсчёта!
2. О переносном ускорении.
Переходим к рассмотрению переносного ускорения We (выр.(3)), которое развивается любой условной точкой жёстко связанной с подвижной системой и совершающей движение вместе с ней как единое жёсткое тело с переносным ускорением We. При этом весь этот набор из трёх членов переносного ускорения (выр.3) реально воздействует на все точки твёрдого тела с его связанными осями в подвижной системе отсчёта и поэтому автоматически просто визуально-формально приписывается и нашей рассматриваемой свободной точке от одной из тех жёстко-связанных с подвижной системой точек, которая в каждый из моментов времени визуально СОВПАДАЕТ по положению с РАССМАТРИВАЕМОЙ НАМИ СВОБОДНОЙ ТОЧКОЙ. Но если переносные ускорения у «жёстко-связанных» точек реальны и объяснимы наличием жёсткой связи как единого материального вращающегося тела, то приписывание этих же самых ускорений нашей свободной точке, никак не связанной с подвижной системой и движущейся самостоятельно в пространстве под воздействием реальных сил, действующих в обеих системах (например, силы гравитации), является полнейшей фикцией (оптической иллюзией), от которой абсолютные уравнения рассматриваемоё точки в сложном движении и надо ОСВОБОДИТЬ, иначе говоря, вычесть это переносное ускорение We из абсолютного реального ускорения точки W, стоящего слева в выр.(1). По той же самой причине необходимо вычесть и кориолисово ускорение Wс.
Посмотрим, что представляют из себя три члена переносного ускорения в выр.(3).
Первый член – это линейное ускорение начала подвижной системы WA, кстати, в общем случае начало подвижной системы может обладать и вектором линейной скорости VA, который также должен быть учтён, но уже в качестве начального значения скорости в дифференциальных уравнениях движения для скорости рассматриваемой точки.
ПЕРЕНОСНОЕ ускорение начала подвижной системы WA (как и вектор скорости начала системы VA ) целиком и полностью приписываются собственному движению рассматриваемой точки (как впрочем и всем точкам условного твёрдого подвижного тела), поскольку само начало подвижной СК считает себя всегда неподвижным и не вращающимся центром (угловую скорость подвижной системе мы назначаем сами с позиций другой, внешней для подвижной системы - инерциальной системы, что справедливо и для любых систем отсчёта, например, также приписывается скорость и ускорение поступательного движения для начала подвижной системы со стороны внешней системы. По правилу механики о допустимости параллельного переноса линейные вектора ускорений и скорости начала системы отсчёта ВПОЛНЕ СПРАВЕДЛИВО приписываются всем точкам условного жёсткого подвижного тела и тут же, заодно, и нашей свободной точке в сложном движении, но уже АБСОЛЮТНО НЕОПРАВДАННО (просто чисто визуальным наложением ускорения точки жёсткого подвижного тела, совпавшей в данным момент с нашей свободной точкой), поскольку реально нет никакой наложенной физической связи между рассматриваемой нами свободной точкой и совпавшей с ней в данный момент «жёсткой» точкой тела подвижной системы. По этой причине простого визуально-формального приписывания нашей рассматриваемой точке линейного ускорения и скорости начала подвижной системы их также надо вычесть в сложном движении из абсолютного ускорения и скорости неподвижной системы.
Второй член переносного ускорения в виде ((dω/dt) ×r) называется в механике вращательным ускорением и есть ни что иное, как вектор дополнительной линейной скорости, возникающий за счёт углового ускорения вращения начала подвижной системы (dω/dt) на дальности r и суммирующийся с вектором круговой скорости (V = (ω × r)) (см. о нём чуть ниже по тексту), правда, только при условии совпадении по направлению векторов углового ускорения и угловой скорости, что, конечно, не всегда выполняется.
Перед началом рассмотрения третьего члена переносного ускорения вспомним правила определения векторного произведения двух векторов и заодно определим, как расположен в пространстве третий член переносного ускорения из выр.(3), равный двойному векторному произведению: (ω × (ω × r)) и своим видом напоминающий выражение для центростремительного ускорения при вращении тела по кругу. Проверим, не оно ли это?
Нелишним будет напомнить о том, что все векторные произведения пар векторов взяты в круглые скобки, вектора в них отмечены жирным шрифтом, и добавлен символ векторного умножения «×», а результатом этого произведения является также вектор, направление которого определяется с помощью правила правой руки (см. это «правило правой руки» в виде справки под выр.(8) в начале предыдущего комментария), а величина (длина) итогового вектора произведения двух векторов может быть определена по правилу раскрытия векторного произведения, описанному ниже.
Например, для выражения, определяющего вектор скорости любой системы точки (V) при её вращении с угловой скоростью (вектор ω) относительно начала системы отсчёта с радиуcом-вектором вращения r определяется векторным произведением: V = (ω × r), в котором длина вектора скорости рассчитывается по выражению для его модуля (операция взятия модуля от вектора в виде вертикальных скобок | V |) векторного произведения в виде:
| V | = | ω | | r | sin(φ),
где угол φ есть угол между вектором угловой скорости (ω) и радиусом-вектором расстояния до рассматриваемо рассматриваемой точки (r) из начала системы отсчёта и, как правило, этот угол равен 90 градусам для чаще всего встречающихся случаев рассмотрения движения в одной плоскости рисунка, когда вектор угловой скорости вращения неинерциальной системы перпендикулярен плоскости рисунка с плоскими траекториями движения точек, например, вращения точки по кругу и направлен вертикально вверх своей стрелкой от плоскости рисунка из начала системы координат на наблюдателя (при этом ЗА ПОЛОЖИТЕЛЬНОЕ НАПРАВЛЕНИЕ ВРАЩЕНИЯ (ω), принято принимать вращение вокруг этого вектора в плоскости рисунка ПРОТИВ ЧАСОВОЙ СТРЕЛКИ). В результате на таком рисунке вектор скорости вращения для точки лежит в плоскости рисунка, является перпендикулярным радиус-вектору расстояния точки от начала координат и направлен при такой положительной скорости вращения влево от радиуса-вектора дальности. В итоге, векторного произведения V = (ω × r) получили вектор скорости вращения скорость вращения (V) точки по окружности, направленный влево по касательной к ней.
Далее раскроем последний член для переносного ускорения из выр.(3), записанного в виде двойного векторного произведения, подставив только что рассмотренный нами вектор скорости для вращающейся по кругу точки (V=(ω × r)): (ω × (ω × r)) = (ω ×V). Раскрывая так же по правилу правой руки векторное произведение (ω ×V) выясняем, что итоговый вектор Wосестремит. = (ω ×V) действительно лежит в плоскости рисунка кругового вращения точки и направлен на начало системы отсчёта и является ничем иным как ОСЕСТРЕМИТЕЛЬНЫМ УСКОРЕНИЕМ при вращении точки с вектором угловой скорости (ω), которое в частном случае чисто плоского движения совпадает с вектором ЦЕНТРОСТРЕМИТЕЛЬНОГО ускорения вращения по кругу:
Wцентростр. = (ω × (ω × r)) = (ω ×V). -это вектор центростремительного ускорения точки …(10)
его величина может быть представлена в плоском круговом вращении разными выражениями:
|W центростр.| = | ω | | ω | | r | = | ω | | V | = | ω |2 | r | = | V |2 / | r | …………...................…(11)
Как говорится, выбирайте любое, подходящее Вам, выражение для центростремительного ускорения в плоском вращательном движении точки.
3. О кориолисовом ускорении.
Выражение для определения кориолисова ускорение (выр.4) выглядит в векторном виде так:
Wс = (2ω × Vr).
Модуль этого векторного ускорения равен: | Wс | = 2|ω| |Vr| sin(ω,Vr). Для него можно применить правило правой руки, но есть ещё более удобное правило Н.Е. Жуковского в следующем виде:
« Проекцию вектора относительной скорости Vr на плоскость, перпендикулярную вектору угловой скорости ω подвижной системы координат, равную |Vr| sin(ω,Vr) следует умножить на 2|ω| и повернуть на угол 90 градусов вокруг вектора ω в направлении вращения, и по этому направлению направить вектор кориолисова ускорения».
Вполне очевидно, что кориолисова ускорения не будет, когда один из векторов нулевой, или же вектор относительной скорости параллелен вектору угловой скорости, т.к. при этом sin(ω,Vr)=0.
Это можно продемонстрировать на примере жителей экватора Земли, где перемещения с линейной скоростью строго в сторону полюсов Земли (поперёк экватора) параллельны вектору угловой скорости вращения Земли и НЕ порождают появления кориолисова ускорения, а вот движение вдоль экватора на восток с относительной Vr приведёт к появлению кориолисова ускорения, направленного к центру Земли точно так же, как и направлена другая составляющая от осестремительного (центростремительного) ускорения (см. выше чуть выше окончание предыдущего 2.раздела) и их совместное «фиктивно" приписываемое свободным телам на Земле, мы вынуждены компенсировать в НЕинерциальных системах (см. выр.5), беря их с обратным знаком и, в итоге, появляется ДОПОЛНИТЕЛЬНОЕ СНИЖЕНИЕ ускорения притяжения тела на экваторе за счёт воздействия «центробежного» и дополнительного «антикориолисова (т.е. направленного в обратную сторону относительно кориолисова ускорения) ускорений. А вот при движении в обратную сторону относительно вектора линейной скорости вращения Земли, т.е. на запад, знак кориолисова ускорения изменится и вектор ускорения будет направлено вертикально вверх, т.е. противоположно гравитационному ускорению, а «антикориолисово» ускорение, будет направлено в обратную сторону - к центру Земли, дополнительно прижимая тело к Земле частично компенсируя центробежное ускорения благодаря эффекту снижения реальной угловой скорости вращения тела относительно Земли из-за наложения дополнительной скорости перемещения против обычной линейной скорости вращения Земли на экваторе. Не забудем о том, что кориолисово ускорение МОЖЕТ ПРОЯВЛЯТЬСЯ ТОЛЬКО ПРИ НАЛИЧИИ УГЛОВОЙ СКОРОСТИ ВРАЩЕНИЯ системы, внося своё дополнительное ускорение пропорциональное величине скорости относительного перемещения.
Если двигаться в северном полушарии Земли, то такое относительное перемещение сопровождается появлением реального кориолисового ускорения, направленного горизонтально в левую сторону относительно вектора линейной скорости, а на южном - в правую сторону, то только из-за того, что люди там ходят вниз головой относительно северян. Это хорошо видно наблюдателя из космоса, например, находящегося над северным полюсом Земли.
А теперь немного о форме этой траектории, вызываемой действием кориолисового ускорения. Влияние ускорения Кориолиса (как и всех видов переносных ускорений, ставших «фиктивными» ускорениями по отношению к свободной точке), имеют знак минус (см. выр.(5)), что и приводит к появлению изогнутой траектории на поверхности Земли, появление которой объясняется не воздействием реального ускорения на свободную точку, а результатом оптическим наложения двух движений - прямолинейного полёта (относительно звёзд) над Землёй и вращательного перемещения под телом подстилающей поверхности Земли, иначе говоря в виде траектории, создаваемой перемещением тени от горизонтально пролетающего с постоянной высотой свободного тела на подстилающую поверхность Земли. При этом, если вектор угловой скорости вращения поверхности положительный, т.е. направлен вертикально вверх, то поверхность вращается справа налево и вектор реального кориолисова ускорения для точек условного твёрдого вращающегося вместе со своими осями тела лежит в горизонтальной плоскости и направлен всё время ВЛЕВО И ПЕРПЕНДИКУЛЯРНО вектору относительной скорости точки, т.е. с поворотом на 90 градусов против часовой вектора скорости тела. Кстати, отсюда и второе название этого кориолисова ускорения – ПОВОРОТНОЕ, поскольку оно всё время стремится повернуть вектор относительной скорости движущегося тела. Но поскольку мы вынуждены применить в уравнении движения во вращающейся системе компенсирующий ОБРАТНО-НАПРАВЛЕННЫЙ вектор «антикориолисова» ускорения, то, в итоге, криволинейная проекция траектории тела на поверхность всё время ФАКТИЧЕСКИ ПОВОРАЧИВАЕТСЯ ВПРАВО от направления движения тела (что неплохо показано в мультиролике в Википедии по теме: Королисово ускорение).
Для подтверждения правильности предлагаемой системы ОТКАЗА от фиктивных СИЛ сравним, обычно вводимую в некоторых учебниках Кориолисову силу инерции, равную Ji кор. = – mi Wc (кор.) (см. выр. 8 и 9) с другой вполне РЕАЛЬНОЙ Силой Кориолиса, равной Fс = (2ω × Vr) m , с которой будет давить (без сил трения) на свободное тело с массой m, например, условная гладкая вертикальная стенка, находящаяся от него с правой стороны с момента начала движения и проходящая, например, по меридиану Земли с севера на юг к экватору и набегающая всё время с правой стороны на это свободное тело, летящее с севера на юг к экватору Земли на высоте не превышающей высоты этой стенки и стремящимся сохранить неизменным положение вектора своей скорости относительно неподвижных звёзд. Этим и объясняется появление реальной правосторонней боковой силы Кориолиса со стороны набегающей стенки на свободное тело, вследствие вращения Земли справа налево (против часовой стрелки) в северном полушарии. И если давжды проинтегрировать только одну эту величину кориолисова ускорения реальной боковой Кориолисовой силы, то получим загибающуюся влево криволинейную траекторию, которая полностью будет скомпенсирована воздействием «фиктивного» «атникориолисова» ускорения, равного кориолисову ускорению, но направленного в обратную сторону со знаком минус и в итоге их взаимной компенсации и будет получена прямолинейная относительно поверхности Земли траектория вдоль меридиана с севера на юг с попаданием в точку прицеливания на экваторе, а не криволинейную, как у свободного тела, не контактирующего с вышеописанной условной стенкой, и реально промахивающегося относительно первоначальной точки прицеливания, расположенной на экваторе до начала движения свободной точки, вследствие убегания этой самой точки за время полёта свободного тела из-за вращения Земли.
Но в современных учебниках по механике перед читателем часто появляются сразу ДВЕ корилисовых силы: фиктивная, несуществующая реально, Сила Кориолиса инерции (Ji кор. = – mi Wc (кор.)), предназначенная ТОЛЬКО для получения правильного результата во вращающейся системе и реальная Сила Кориолиса (Fс = (2ω × Vr) m), которая может возникнуть только при наличии физической связи рассматриваемого передвигающегося тела с поверхностью Земли, как например, у рек с правой стороны в северном полушарии Земли, так и в вышерассмотренном полете свободного тела с наложенной на него физической связью в виде условной гладкой стенки. И вот надо всё это объяснить и растолковать, что одна из них фиктивная, а другая – реальная, хотя и отличаются друг от друга добавлением в названии первой фиктивной силы слова «сила инерции». Ну не сложновата ли эта головоломка для учащихся?
А ведь, если убрать все эти фиктивные «Силы инерции» (переносную и кориолисову), заменив их фиктивными орицательными "антиускорениями", то всё станет гораздо понятнее и проще, а в уравнениях движения реальная сила кориолиса (Fс = (2ω × Vr) m) сможет появиться только при условии наложении физической связи на рассматриваемое относительное движение тела, зато фиктивное кориолисово ускорение (с предлагаемым названием "антикориолисово" ускорение) пропишется навсегда (как и "антипереносное" ускорение) во втором законе Ньютона для движения тел в неинерциальных системах (см выр.(5)).
P.S. Более подробное обсуждение кориолисова ускорения, вызывающее повышенный интерес у некоторых знатоков механики, в связи c множителем 2 в кориолисовом ускорении, рассмотрим позже.
Георгий 16.03.2020 12 час.05мин. Времы моск.
О выводе геометрическим методом выражения для Кориолисова ускорения
Опишу непростой пройденный путь при попытке геометрического вывода формулы для кориолисова ускорения.
В предыдущем комментарии этот вывод легко и просто был произведён с применением чисто формального математического метода дифференцирования вектора относительной скорости, что лишь подтверждает всю мощь математического аппарата векторной алгебры, а именно:
Wс = (2ω × Vr). ………………………………………………………………….. (1)
В основу геометрического подтверждения этого выражения для реального ускорения Кориолиса было решено положить метод доказательства от уже заранее известного выражения к его геометрическому обоснованию и подтверждению вплоть до коэффициента 2 в выр.(1).
Итак, допустим, что нам известно конечное выражение сложной функции времени (f), которая является в первом приближении векторным произведением двух переменных Wc ~= f (ω × Vr). Найдём ее точное выражение геометрическим способом, применив для этого вывода правило для определения дифференциала от произведения двух функций времени: как произведение дифференциала от первой функции на вторую плюс произведение первой функции на дифференциал от второй:
Δ (ω × Vr) = Δ (ω) × Vr + ω × Δ (Vr). …………………………………………… (2)
где: Δ(…) – операция сообщения допустимого для данной функции небольшого по величине приращения, от которого мы потом избавимся, поделив на соответствующее ему небольшое приращение времени Δ(t), и после устремления величины Δ(t) к нулю, заменим отношения приращений Δ(…)/Δ(t) на выражение для производной d(…)/d(t) от функции, которая и будет равна УСКОРЕНИЮ Кориолиса.
Для геометрического вывода на плоской вращающейся поверхности (с угловой скоростью ω) и тела, имеющего физическую связь с этой поверхностью (в виде трения без проскальзывания) и перемещающегося относительннеё в любом возможном направлении (с линейной скоростью Vr). Нам даже не понадобится геометрический рисунок по причине его элементарности в виде обычной окружности как годографа (от вращения по кругу) конца радиуса-вектора r (или его же эквивалента - вектора относительной скорости Vr с длиной вектора Vr Δ(t), равной длине вектора r ), описывающего эту самую окружность, а в центр этой окружности поставим вертикальный кол в виде вектора угловой скорости вращения (вектор ω, вращающийся для определённости с положительной угловой скоростью, т.е. против часовой стрелки). Вот и вся заготовка для мысленного рисунка.
С начала была предпринята довольно быстрая и успешная попытка с применением вышеописанного правила сложения двух независимых приращений по ω и Vr для геометрического обоснования выр.(1) в случае, когда вектор скорости Vr был направлен вдоль радиуса-вектора дальности (R большое) из центра вращения плоской поверхности, расположенного, где-то внизу плоскости рисунка, т.е. вне вышеописанного малого круга (с малым радиусом r). Не буду его описывать сам вывод, т.к. это будет сделано позже на примере малого круга с радиусом r. Метод реализовался легко и просто, т.е. в случае направления относительной скорости тела Vr вдоль радиуса-вектора дальности (R большое) никаких проблем не возникло.
Но когда была предпринята аналогичная попытка вывода выражения тем же самым способом, но только случае, когда вектор скорости Vr, направлен перпендикулярно к радиусу-вектору дальности (R большое) вывод застопорился и никак не поддавался. То, что элементарно и очевидно срабатывало в первом случае наповал не срабатывало во втором случае тангенциальной скорости по отношению к радиусу-вектору (R большое) из центра вращения.
И тут пришло озарение, состоящее в том, что вектор скорости вращения подстилающей плоской поверхности ω надо перенести из своего истинного центра вращения подстилающей поверхности в центр масс самого движущегося с линейной скоростью Vr тела! Ведь мы так фактически и поступаем, когда применяем правило правой руки для определения векторного произведения, совмещая в одну точку вектора угловой и линейной скоростей!
Вот тогда геометрический вывод подтверждается на круге малого радиуса r с его центром в самой подвижной рассматриваемой точки даже независимо от направления вектора скорости Vr в силу полной круговой симметрии самого малого вращающегося круга, из центра которого и направлен вектор относительной скорости перемещающегося по поверхности тела.
Предпосылкой для такого действия переноса вектора вращения ω явилась и сама методика простого вывода по первому удачному варианту геометрического вывода, когда Vr был направлен ВДОЛЬ большого вектора-радиуса R вращения тела, проведённого из далёкого истинного центра вращения поверхности. Тогда при выводе одной из равноценных составляющих формулы, равной (Δ (ω) × Vr), получаемой ТОЛЬКО ЗА СЧЁТ ПРИРАЩЕНИЯ по угловой скорости (Δ (ω)) приходилось брать разницу В ДЛИНАХ ПУТЕЙ, ПРОХОДИМЫХ ПРИ ВРАЩЕНИИ ПО КРУГУ ЦЕНТРОМ МАСС ДВИЖУЩЕГОСЯ ТЕЛА, И КОНЦОМ ЕГО ЖЕ ВЕКТОРА ОТНОСИТЕЛЬНОЙ СКОРОСТИ, ОТСТОЯЩИМ ОТ НЕГО ВПЕРЁД НА РАССТОЯНИЕ малого-радиуса вектора r и при этом за счёт ТОЛЬКО ДЛИНЫ САМОГО ВЕКТОРА r И ПОЯВЛЯЛОСЬ ПРИРАЩЕИЕ ЛИНЕЙНОЙ ГОРИЗОНТАЛЬНОЙ СКОРОСТИ КОНЦА ВЕКТОРА r ОТНОСИТЕЛЬНО НАЧАЛА САМОГО ВЕКТОРА, ВЫЗАННОЙ РАЗНИЦЕЙ В ЛИНЕЙНЫХ СКОРОСТЯХ ВРАЩЕНИЯ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ (на базе длины вектора малого вектора r ).
С учётом вышесказанного, осталось только произвести геометрический вывод выражения для корилисова ускорения по методике взятия дифференциала (приращения) от произведения по выр.(2), используя мысленный круг с малым радиусом-вектором r и его же эквивалента - вектора относительной скорости Vr с длиной вектора Vr Δ(t). Напомним правило для взятия дифференциала от произвеения двух функций времени:
Δ (ω × Vr) = (Δ (ω) × Vr) + (ω × Δ (Vr)). ………………………………………. (2)
Определим оба независимых приращения в правой части выр.2, считая, что первое приращение происходит только за счёт поворота вектора относительной скорости на небольшой угол, равный (ω Δ(t)) за счёт ТОЛЬКО ВРАЩЕНИЯ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ. При этом нас интересует ТОЛЬКО ВРАЩАТЕЛЬНАЯ ЧАСТЬ ОТ ЭТОГО движения подстилающей поверхности, поскольку плоскопараллельноя поступательная часть этого движения подстилающей поверхностиникаких эффектов в виде ускорений не даёт и её можно НЕ РАССМАТРИВАТЬ, а вот это и означает, что вращение можно рассматривать относительно НАЧАЛА ЦЕНТРА МАСС ДВИЖУЩЕГОСЯ ТЕЛА в виде вектора вращения ω при радиусе-векторе r, полностью совпадающему, например, с вектором относительной скорости r = Vr и пока без его приращения по времени.
Тогда, раскрывая векторное первый член приращения в выр. (2), т.е. произведение Δ (ω) × Vr, получим вектор дополнительной линейной скорости ΔVr, конца вектора Vr, возникаюший при повороте конца вектора Vr в горизонтальной плоскости подстилающей поверхности с угловой скоростью ω, и это лежащий вектор приращения скорости (ΔVr) в горизонтальной плоскости расположен нормально к концу радиуса-вектора вращения r и представляет собой аналог вектора окружной скорости конца радиуса-вектора при равномерном вращении по кругу, т.е.:
ΔVr1 = (Δ(ω) × Vr) = (ω Δ(t) × Vr) = (ω × Vr) Δ(t). …………..…….………….(3)
Вторую составляющую в выр.(2) получим за счёт другого приращения (независимого от первого) по смещению вперёд (относительно центра рассматриваемого нами круга) самого вектора скорости линейной Vr вдоль самого себя на малое расстояние, равное приращению пути за период времени Δ(t), т.е. Δ (Vr) = Vr Δ(t) и которое сопровождается появлением дополнительного приращения боковой линейной скорости конца вектора относительной скорости ТОЛЬКО ИЗ-ЗА ПРИРОСТА РАДИУСА ВРАЩЕНИЯ на величину Vr Δ(t), поскольку возрастает скорость вращения подстилающей поверхности за счёт смещения целиком самого вектора относительной скорости Vr на приращение величиной, равной Δ (Vr) = Vr Δ(t). По правилу раскрытия векторного произведения получим вторую составляющую кориолисова ускорения в виде:
ΔVr2 = (ω × Δ(Vr) = (ω × Vr Δ(t)) = (ω × Vr) Δ(t). …………………………. (4)
Просуммируем оба коллинеарных вектора приращений из выр.(3 и 4) , направленных в одну сторону, влево по нормали к концу вектора скорости Vr, в соответствии с выр.(2) для взятия дифференциала:
ΔVr полн. = ΔVr1 + ΔVr2 = (ω × Vr) Δ(t) + (ω × Vr) Δ(t) = (2ω × Vr) Δ(t). …... (5)
Поделив обе части выр.(5) на Δ(t) и взяв предельный переход за счёт устремления Δ(t) к нулю, получим окончательное выражение для кориолисова ускорения, совпавшее с выр.(1), полученным ранее с применением методов векторной алгебры:
Wc = Lim| Δ(t) ->0 (ΔVr / Δ(t)) = (2ω × Vr). ….……………………………………..(6)
Вот так, совершенно просто (даже без реального, а лишь воображаемого рисунка!), удалось геометрическим способом получить правильное выражение для Корилисова ускорения с учётом правила взятия дифференциала от некоего исходного векторного произведения двух параметров (ω,Vr) для тела перемещающегося над вращающейся поверхностью при полной независимости выр.(6) от направления вектора относительной скорости по направлению относительно подстилающей поверхности.
И ВСЁ-ТАКИ ЦИФРА ДВОЙКА (2) В КОРИОЛИСОВОМ УСКОРЕНИИ НЕОБХОДИМА И ЕЁ ВЕЛИЧИНА НИКАК НЕ ЗАВИСИТ ОТ НАПРАВЛЕНИЯ ВЕКТОРА ОТНОСИТЕЛЬНОЙ СКОРОСТИ ТЕЛА по отношению к подстилающей вращающейся поверхности.
Поэтому все попытки некоторых авторов доказать переменность числового коэффициента (2) перед вектором угловой скорости ω в выражении (6) для Кориолисова ускорения или замену 2 на 1 , с моей скромной точки зрения, АБСОЛЮТНО НЕСОСТОЯТЕЛЬНЫ и демонстрируют лишь их многочисленные заблуждения и наукообразные плутания в попытке обосновать другие значения коэффициента при ω на примере многочисленных и малопонятных стереометрических рисунков.
Вот, например, некий автор А.А.Астахов, посвятил этой проблеме целую книгу, основная часть которой и была посвящена анализу кориолисова ускорения. (http://www.sciteclibrary.ru/texsts/rus/stat/st5379.pdf ).
В аннотации к статье автор пишет:
«Точное значение силы Кориолиса не равно удвоенному произведению угловой скорости переносного вращения на линейную скорость относительного радиального движения. Численный коэффициент в этом произведении всегда меньше двойки. Отличие тем больше, чем меньше радиус переносного движения. С увеличением радиуса переносного вращения коэффициент стремится к двум. Ускорение Кориолиса, определяющее геометрическое приращение поворотного движения равно половине классического ускорения Кориолиса. При равномерном относительном движении перпендикулярном радиусу сила и ускорение Кориолиса не проявляются.»
Как видим, автор не догадался перенести вектор вращения в центр масс движущегося тела (что можно и надо делать обязательно в полном соответствии с правилом раскрытия векторного произведения (2ω × Vr) ) и он, как и я в начале, утонул в дебрях «движения, перпендикулярному радиусу-вектору, проведённому из центра вращения в центра масс тела».
При этом попутно автор, видимо, не хочет говорить (а скорее и не подозревает) о возможности существования реальной "Силы Кориолиса", определяемой по выражению: Fкор = (2ω × Vr) m. Именно реальным воздействием которой и объясняются эффекты подмывания правых берегов у всех рек северного полушария Земли независимо от направления течения, а также закручивание атмосферных циклонов во вращение против часовой стрелки (см. предыдущий комментария от 16.03.2020.)).
В качестве подтверждения другого моего предложения о необходимости УСТРАНЕНИЯ из механики ВСЕХ ФИКТИВНЫХ «СИЛ ИНЕРЦИИ», к коим и относится незаслуженно упоминаемая во многих учебниках ОТРИЦАТЕЛЬНОЕ И ПОЛНОСТЬЮ ФИКТИВНОЕ (подчёркнуто для А.А.Астахова) Кориолисова сила инерции (Jкор.= – (2ω × Vr)m) было предложено ОТКАЗАТЬСЯ ОТ ВСЕХ ФИКТИВНЫХ СИЛ, ОСТАВИВ ВМЕСТО НИХ В НЕИНЕРЦИАЛЬНЫХ ВРАЩАЮЩИХСЯ СИСТЕМАХ ЛИШЬ ИХ ФИКТИВНЫЕ «АНТИУСКОРЕНИЯ» (например, «антикориолисовое»: Wантикор.= – (2ω × Vr)).
И вот этому очередное наглядное подтверждение из книги этого автора в виде цитаты из его статьи, (извините за длинную цитату):
«И в геометрических, и в аналитических выводах ускорения Кориолиса во всех современных учебниках, а также в работах классиков теоретической механики фигурирует удвоенное именно геометрическое, т.е. реальное ускоренное приращение траектории поворотного движения в направлении линейной скорости переносного движения. Примеров этому в нашей работе приведено достаточно много. И самый яркий из них по представлению физической сущности классической версии явления Кориолиса это определение удвоенного ускорения Кориолиса, как линейного ускорения через линейный путь, пройденный с ускорением Кориолиса.
Такие выводы есть, в том числе и в справочной литературе по физике. Причём в них не оговаривается, что это ускорение фиктивное.*1)
Фиктивной, по мнению классической физики, является лишь сила Кориолиса.*2)
Причём не половина силы Кориолиса, а именно вся её физическая величина...
Более того, ошибка определения ускорения поворотного движения прочно вошла в математический метод дифференцирования криволинейного движения по приращению его координат. Приращение скорости это всегда приращение расстояния, пройденного с ускорением, но приращение координат не всегда соответствует приращению этого расстояния. Поэтому вторая производная от приращения координат не всегда соответствует реальному геометрическому ускорению криволинейного движения. Классическое дифференцирование приращения криволинейного движения этого не учитывает.»
*1) К вашему сведению, это ускорение и есть самое настоящее реальное (а не фиктивное, как вам кажется), т.е.реальное ускорение точек условного твёрдого вращающегося тела со знаком плюс, а не фиктивное со знаком МИНУС, вводимое в уравнения в неинерциальной системе для устранения несправедливо и чисто визуально наложенному на свободное тело, которое никакими физическими связями не привязано в точкам вращающегося условного тела!
*2) Это так называемая «сила Кориолиса инерции». И не надо путать двух разных «баранов»: ранее названную полностью фиктивную «сила Кориолиса инерции» (со знаком МИНУС) и просто «Силу Кориолиса» (без добавления слова «инерции» и со знаком ПЛЮС), которая вполне реальна и о существовании которой автор даже не догадывается, возясь по-прежнему с официальной (из учебников) отрицательной по знаку и фиктивной «силой Кориолиса инерции» и которую он ещё и вдобавок УСЛОВНО разделил на две части (вдоль радиуса вектора и поперёк него), усмотрев в первой из них реальность, а во второй, с выводом выражения для которой он так и не смог справиться, – фиктивность. С чем мы его и поздравляем. Именно в этом-то и небольшом отличии в названии двух Сил Кориолиса и состоит грубая ошибка автора, не различившего две разных противоположно направленных силы: фиктивную "Силу Кориолиса инерции"(отрицательную по знаку) и реальную "Силу Кориолиса"(положительную по знаку).
Вот так от мешанины из ДВУХ СОВЕРШЕННО РАЗНЫХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ Кориолиса, превратившихся для автора статьи в одну единую «фиктивную и наполовину реальную» НОВУЮ гибридную Силу Кориолиса, чудесным образом совместившей в себе фиктивную «Кориолисову силу инерции» СО ЗНАКОМ МИНУС (на слово «инерции» в учебниках все уже давно как-то перестали обращать внимание) и опрометчиво введённой в учебниках (видимо, для того, чтобы всех запутать окончательно букетами из разнообразных «Сил инерции»), и вполне реальную Силой Кориолиса (без ключевого слова «инерции» И СО ЗНАКОМ ПЛЮС перед тем же самим реальным кориолисовым ускорением), возникающей вполне реально при наличии физических связей с вращающейся поверхностью Земли (например, при подмывании одного из берегов рек и эффект закручивания циклонов в вихри). Автор, не разобравшись с этими двумя АНТИПОДАМИ из двух Сил Кориолиса противоположно направленными (причём одна из них фиктивная, а другая реальная), перевалил со своей «больной головы» на «здоровую голову» математики все свои проблемы вывода, бросив тень на метод дифференцирования (видите ли он «не всегда соответствует» ожиданиям автора). Надо же найти виноватого, вот он и найден в виде метода дифференцирования.
Надеюсь, молодёжи ещё более стал понятен предлагаемый мною принцип «ликвидации как класса» целого «зоопарка» «Сил инерции» (так любезных Астахову, что он за них «горой» против всех и вся, и даже начинает их считать вполне реальными!), и которым предлагается объявить их тотальную ликвидацию и подвергнуть наказанию в виде «пожизненного цика на гвоздях», как во второй серии фильма «Кин-дза-дза»*), не в меру расплодившихся на страницах учебников механики, и как следствие, необходимо одновременное ЗАКРЕПЛЕНИЕ ЗА ФИКТИВНЫМИ УСКОРЕНИЯМИ (как первоисточника всех этих бед в виде "Сил инерции") вполне почётного и заслуженного звания «АНТИУСКОРЕНИЯ» (в данном случае - «антикорилисова ускорения» со знаком МИНУС: Wантикор.= – (2ω × Vr)) и "антипереносное" ускорение (Wантипер. – также со знаком минус (относительно реального переносного ускорения точек твёрдого тела идущих вседа со знаком плюс) в неинерциальных вращающихся системах для нормальной работы второго Закона Ньютона при расчёте движения свободного тела.
*) Примечание, для разрядки атмосферы, немного о моём любимом фильме Г.Данелии: «Кин-дза-дза». Редактор MS Word всё упорно пытался заменить мои прописные буквы слова «цик» на заглавные «ЦИК», так же как и обратно прочитанное слово «кц» (обычные спички в фильме), т.е. «цк» на "ЦК". Ай да Георгий Данелия, не зря переписывал несколько лет для обхода цензуры, свой сценарий, весивший со всеми вариантами 5 кг! Съёмки фильма в пустыне Каракум были тяжёлыми и многие не снявшиеся по разным причинам в этом фильме актёры (Вахтанг Кикабидзе, Леонид Ярмольник, Валентин Гафт), думаю не раз пожалели об этом, а вот Юрий Яковлев был готов сняться у Данелии хоть на Луне. Даже когда он лежал в больнице, то в ответ на неожиданное предложение от Данелии сняться в фильме и «Что надо уже сейчас начинать сниматься»), Яковлев ответил: «Хорошо, я завтра выйду!». Талантливый дуэт ещё болезненного на вид Юрия Яковлева и плутоватого, добродушного и надутого (от осознания своего высокого происхождения) Евгения Леонова украшает этот фильм, да и Станислав Любшин им под стать. По началу фильм (выход на экран в 1987г) многие не приняли и только по прошествии некоторого времени люди оценили эту притчу об убогой действительности общества с дифференциацией по цвету штанов (оранжевые в фильме и малиновые пиджаки в перестройку) Кстати, название фильму дал не грузин Данелия с его любимой травой Закавказья - кинзой, а совсем случайно «выдал» Евгений Леонов, когда к нему, раскачивающемуся в гамаке внутри прохладпного пепелаца (космического корабля, больше напоминающего конический чугунный литой летающий "сортир"), подсел Станислав Любшин и спросил, «что в порт-феле» у Леонова, то тот сначала раздумчиво повторил окончание последнего слова «Феле-феле-феле», а затем ответил : «Зелень, кинза» и давай распевать «Кин-дза-дза-дза…» Всю дорогу он пел, а название осталось»…Так исчез первоначальный вариант названия фильма: «Космическая пыль»… Это отрывок из статьи Марии Конюковой из журнала «Тайны СССР №3 за 2020г., стр 16-17».
Однако, продолжим в назидание молодёжи демонстрацию этих заблуждений А.А.Астахова и приведём ещё одну фразу из рассматриваемой статьи, где автор обнаружил противоречия в Кориолисовой силе, которую он, видимо, знает только в виде ОДНОГО ФИКТИВНОГО ВАРИАНТА и даже не замечает знака ПЛЮС в реальной Кориолисовой силе ( а не фиктивной Кориолисовой силы инерции, кроме которой автор ничего не знает), когда в примере известного физика Фейнмана с движением человека по радиусу вращающейся карусели и испытывающего на себе воздействие вполне реальной силы Кориолиса вынужден наклоняться вбок для компенсации «закручивающуей силы», чтобы не упасть. Оцените всю глубину искреннего недоумения автора по этому поводу:
«Начнем с того, что выясним, почему закручивающую силу, которая реально изменяет угловой момент вращательного движения, Фейнман ассоциирует с силой Кориолиса, которая с точки зрения классической физики, являясь силой фиктивной, не может изменить момент импульса в принципе.
Фейнман пишет: ≪В действительности мы хотели бы узнать, какую боковую силу должен прилагать человек, чтобы двигать массу m со скоростью Vr=dr/dt. Как видите, она равна Fк = 2ωVr m ≫.
Фактически это означает, что двигая что-то по радиусу необходимо подстраиваться под вращающуюся систему, синхронизируя вращение движущегося вдоль радиуса тела с исходным переносным вращением за счет ≪обычной≫внешней боковой силы. В классической же физике «Сила Кориолиса» считается ФИКТИВНОЙ СИЛОЙ ИНЕРЦИИ. *)
Таким образом, Фейнман в своем выводе фактически противоречит самому себе и классической физике, определяя силу Кориолиса как реальную силу, поддерживающую переносное вращение движущегося радиально тела с исходной угловой скоростью, чтобы его вращение при радиальном движении соответствовало бы прежнему переносному вращению. И это противоречие вполне оправдано, т.к. это есть объективная реальность, которую не могут игнорировать даже сторонники классической модели поворотного движения.»
*) В классической физике ФИКТИВНОЙ СИЛОЙ ИНЕРЦИИ является не «Сила Кориолиса», , а «Сила Кориолиса ИНЕРЦИИ» (со знаком МИНУС!), фиктивная и направленная в обратную сторону по отношению к вполне реальному кориолисову ускорению (а заодно и к реальной "Силе Кориолиса")
Поэтому противоречит классической физике не Фейнман , а Вы, товарищ А.А. Астахов, не заметив как знака плюс в выражении Фейнмана (Fк= 2ωVr m.), так и невнимательно прочитав название силы: "Сила Королиса", но отнюдь не "Сила Кориолиса ИНЕРЦИИ". Хотя в вашем понятии, кроме фиктивной силы Кориолиса другой кориолисовой силы быть и не может!
Вот так А.А.Астахов, автор книги, посвящённой, в основном, анализу кориолисова ускорения вообще не знает и даже не догадывается о возможном существовании другой, реальной "Силы Кориолиса" (но не «инерции») .
А откуда тогда, разрешите спросить его, берётся реальное подмывание правых берегов рек и закручивание циклонов против часов в северном полушарии разве от фиктивной «Силы Кориолиса инерции»? Конечно же НЕТ, не от неё, а от реальной "Силы Кориолиса" со знаком плюс перед кориолисовым ускорением и с направлением действия в левую сторону (в северном полушарии) от направления скрости относительного движения, поворачивая вектор относительной скорости в плоскости вращающейся поверхности Земли всё время по нормали ВЛЕВО от направления вектора относительного движения.
Вот теперь, дорогой читатель, и оцените всю реальную и назревшую необходимость предложенной выше мною реформы в терминологии СИЛ И УСКОРЕНИЙ (см. мой комментарий от 16.03.2020г), если такой вполне себе нагловатый и считающий себя непогрешимым, автор, позволяющий себе критиковать ВСЕХ И ВСЯ, не взирая на лица и звания, ( и даже операцию дифференцирования умудрился между делом упрекнуть в неточнсти ) элементарно запутался в четырёх соснах из двух взаимно противоположных по направлениям Кориолисовых ускорений (реального и фиктивного, со знаком минус) и двух Сил Кориолиса (реальной и фиктивной с обязательным словом в названии «инерции» и со знаком минус перед ускорением)!
Однако автор выпустил ещё и книгу под названием: Александр Астахов «Физика. Порядок вещей, или Осознание знаний. Книга 2», «Издательские решения», где продолжил эту тему о фактической Силе Кориолиса, выдав «на гора» ещё одного уродца в виде Силы «Кориолиса-Кеплера», как он её называет:
«Поскольку в классической динамике вращательного движения понятие об обычной истинной силе Кориолиса-Кеплера отсутствует, то в классической физике родилась самая странная сила не только из всех сил инерции, но и самая странная из всех обычных сил!!! Классическая сила Кориолиса это либо, полу фиктивная обычная сила, либо, полу обычная фиктивная сила. Недаром физики всех времён и народов, начиная со времён Кориолиса, до сих пор спорят, реальна ли сила Кориолиса или же это только иллюзорная сила инерции.»*)
*) Вместо того, чтобы сообразить и умножить РЕАЛЬНОЕ Кориолисово ускорение (точек условного твёрдого вращающегося тела) на массу тела и получить вполне реальную Силу Кориолиса ( Fкор.= (2ω × Vr) m), направленную противоположно "Силе Корилиса инерции" (Fкор.инерции= – (2ω × Vr) m), автор придумал новый гибрид: «силу Кориолиса-Кеплера», (видимо, с заменой множителя 2 на 1), испытывая трудности с геометрическим выводом для ускорения Кориолиса в тангенциальном (поперечном) направлении относительно радиуса-вектора. Знай наших…
Однако у меня к автору книги: «А.А.Астахов Физика Порядок вещей, или Осознание знаний. «Издательство», 2017г.» имеется совсем другой и особый счёт, ибо всё вышеизложенное о его взглядах можно было бы простить автору списать на ошибки и заблуждения, которые можно только отметить (кто из нас не заблуждается или не ошибается – нет таких (в том числе имею в виду прежде всего самого себя). И мой тон был бы совершенно другим в вышеизложенных строках по отношению к автору и более спокойным и выдержанным. Однако сделано это сознательно, покольку есть за что публично наказать.
А вот за другие «прегрешения» хотелось бы спросить уже с автора по «полной программе», поскольку уже с начальных страниц своего опуса, посвящённых разбору Сил инерции, он рьяно набросился на уважаемого мною доктора технических наук, профессора кафедры теоретической механики Нурбея Владимировича Гулиа, написавшего, на мой скромный взгляд прекрасную небольшую книгу под названием «ИНЕРЦИЯ» Издательство «НАУКА» Москва 1982г. 152 стр.» Под эгидой «Академия наук СССР» Серия «Наука и техничесий прогресс» , ответственным редактором которой был, известнейший в области механики, академик А.Ю.Ишлинский. И какая же муха укусила этого Астахова, написавшего всякие гадости про классические взгляды Нурбея Владимировича по вопросам механики. Да под каждым словом небольшой, но безупречной книги Гулиа «ИНЕРЦИЯ» я подпишусь без всяких оговорок, т.к. в ней дан великолепный исторический обзор понятия инерции от античной механики до теории относительности, кратко, но весомо и понятно, чего не могу сказать об опусе словообильного Астахова.
Вообще-то нападки на тексты популярных книг Н.В.Гулиа о механике, силах и инерции вызваны со стороны А.А.Астахова явным НЕСОВПАДЕНИЕМ его представления и Силах инерции с классическим походом к ним как к чисто фиктивным, твёрдо проводимым и известным академиком А.Ю.Ишлинским, А вот для Астахова Силы инерции с одной стороны,чтобы не придпрались к нему, для него фиктивны, но чисто формально (как бы на словах), а с другой, гораздо большей, он считает их, как ни странно, вполне существующими и где-то даже реальными! И главное при этом, что он вместо того, чтобы все появления инертности в механике объяснять врождённым СКАЛЯРНЫМ СВОЙСТОВМ ИНЕРЦИИ МАССЫ ТЕЛА , заменяет для себя существованием почти реальных для него ВЕКТОРНЫХ НЕСУЩЕСТВУЮЩИХ И ФИКТИВНЫХ СИЛ ИНЕРЦИИ с радостью подхватив слова Ньютона в "Врождённой силе материи" при объяснении СВОЙСТВА ИНЕРТНОСТИ ТЕЛА. Такой вот эклектизм в одной голове в отношении к Силам инерции!
И как только он не называет Н.В.Гулиа: и «ярым сторонником фиктивности сил инерции» и что «слова Гулиа ( «…Сил инерции нет, не было и не может быть, потому что в существующей механике им места нет») - это логика типа: этого не может быть, потому что не может быть никогда. Может быть, профессор имел в виду не саму реальную действительность, а ее математическое описание?» и «высказывание Гулиа, скорее всего, следует понимать, как полное отрицание сил инерции в реальной природе».*)
*)Моё примечание: А как же может быть иначе иначе, если они и есть самые что ни на есть фиктивные в неинерциальных системах!
А на примере рассмотрения вращения Луны вокруг Земли дело дошло даже до смешного: Гулиа утверждает, что центробежная сила НЕ ПРИЛОЖЕНА к Луне, естественно, рассматривая её вращение в инерциальной невращающейся системе относительно центра масс Земли, а автор возражает ему следующим перлом, даже не разобравшись в какой системе отсчёта идёт анализ вращения (да, в неинерциальной земной системе к Луне вынужденно приложено ФИКТИВНОЕ «центробежное ускорение» (или «антицентростремительное» ускорение), на что Астахов глубокомысленно возражает, даже не представляя себе разницу между системами отсчёта:
«А поскольку небесные тела реально подталкивает(?) друг к другу вполне материальное поле тяготения, но при этом они не падают друг на друга, то надо полагать, что они сопротивляются ему при помощи вполне реальной центробежной силы».*)
*) Примечание: А может быть, т. Астахов, от того что у Луны есть соотвествующая по величине орбитальная скорость, которая и не позволяет ей рухнуть на Землю! А не благодаря несуществующаей в реальной действительности ФИКТИВНОЙ ЦЕНРОБЕЖНОЙ СИЛЫ! Поищите-ка её в инерциальной системе: её там никогда и не было, кроме ЕДИНСТВЕННОЙ силы притяжения Луны к Земле! И вот благодаря наличию орбитальной скорости Луна, ПАДАЯ ВСЁ ВРЕМЯ на Землю под воздействием ЕДИНСТВЕННОЙ силы притяжения к Земле лишь РАЗВОРАЧИВАЕТ ПО НАПРАВЛЕНИЮ свой вектор орбитальной скорости успевая пролететь вбок, по касательной к радиусу-вектору, направленномк на Землю. , что и приводит к эллипитческой орбите вокруг Земли (почти круговой). Не будет скрости и Луна прямиком, как сорвавшийся лифт, полетит прямо к Земле. Это вам для ОСОЗНАНИЯ и соотвественно для вашего ПРОСВЕТЛЕНИЯ.
Или вот эта наглость зазанавшегося и непогрешимого, а на деле безграмотного автора:
«Как можно утверждать, что он (Гулиа) всё и всем доказал, если с другой стороны можно со сто процентной уверенностью сказать, что сам Гулиа ничего толком не знает о природе инерции. И это не голословное утверждение. На сегодняшний день природа инерции официальной наукой, приверженцем которой является Гулиа, не установлена. Не известны и революционные работы самого Гулиа о природе инерции. Все его нынешние доводы не выходят за рамки средней школы.» *)
*) Природу инерции можно и не знать! Достаточно её лишь привильно учитывать, но грамотно, без вывиха в мозгах.! А по-моему скромному мнению, Вы сами и есть полное невежество и ничтожество, мнящее из себя знатока механики. Позор на уровне средней школы. Далее не буду продолжать, вполне хватит вышесказанного. Это у Вас самого , товарищ Астахов, знания не выходят за рамки средней школы!
И всё это о Докторе технических наук, участвующему в разработке оригинальных накопителей кинетической энергии для транспорта (http://nt.ru54.com/ac/gnv/index.html ) и супервариаторе для них (http://n-t.ru/tp/ts/sv.htm).
P.S. Уважаемый А.А.Астахов! Не надо ничего писать на данный сайт, ответа не будет. Поскольку я стою на страже научности данного сайта (выполняю общественное поручение), то Ваше присутствие на нём объявляю «persona non grata» …
А Вам не кажется, что надо бы извиниться перед уважаемыми людьми (перед Н.В.Гулия, например), что несколько пробудит Вашу подуснувшую совесть и загладит ошибки и заблуждения. Отталкивайтесь, пожалуйста, "от осознания и просветления" (по В.Высоцкому). Вот мне, например, хоть и стыдно за мои ошибки и несдержанности, допущенные мною на этом сайте, но нахожу же я в себе силу признать их. Поверьте, все ошибаются - это естественно, а у Вас, честно говоря, есть талант и глубокое мышление, но Вас одолевает гордыня, разрешающая Вам без огляки верить в Вашу непогрешимость и нападать на всех и вся. Боритесь с неправильными идеями, а не с людьми их высказавшими. После того, что Вы узнали о своих заблуждениях, главное сделать правильные выводя для себя и начать с раскаяния. Но не все могут побороть в себе этот самый страшный грех падшего человека - СОБСТВЕННУЮ ГОРДЫНЮ. Если Вы её сейчас преодолеете, не сделаете первый шаг и не раскаетесь, то она сожрёт Вашу бессмертную душу и погубит Вас окончательно... Вспомните последние годы Л.Толстого, его гордыню. Одумайтесь, пока не поздно, покайтесь. И с новыми силами принимайтесь за новые работы, только без наскоков на других и никогда не забывайте о слабости нашего ума, не возгордитесь, иначе - конец личности. Будьте благоразумны...
P.S. Следующий комментария будет о трактовке трёх законов Ньютона.
Георгий 21.03.2020г 23ч25мин.
К вопросу о трёх основных законах Ньютона
Вернёмся ещё раз к трём законам Ньютона и рассмотрим их с точки зрения инженера-механика.
Перед первым законом Ньютон ввёл Определение III :
« Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения.»
Первый закон Ньютона
Для примера вариант текста Первого закона самого Ньютона из «Начал» в переводе А.Н. Крылова:
«Всякое тело продолжает пребывать в своём состоянии покоя или равномерного прямолинейного движения, пока приложенные силы не понудят его изменить это состояние».
Эта сила всегда пропорциональна массе, и если отличается от инерции массы, то разве только воззрением на неё. От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому «врождённая сила» могла бы быть весьма вразумительно названа «силою инерции». Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко: и как сопротивление и как напор. Как сопротивление – поскольку тело противится действующей на него силе, стремясь сохранить своё состояние; как напор - поскольку то же тело, с трудом уступая силе сопротивляющегося ему препятствия, стремится изменить состояние этого препятствия. Сопротивление приписывается обыкновенно телам покоящимся, напор – телам движущимся. Но движение и покой, при обычном их рассмотрении, различаются лишь в отношении одного к другому, ибо не всегда находится в покое то, что таковым простому взгляду представляется.» Конец цитаты из «Начал».
Однако в Определении III и Законе не очень подчёркнута, на мой взгляд, очень важная особенность свойства инерции тела – её пропорциональность массе тела. По-моему, можно изложить первый закон, подчеркнув роль величины массы тела, хотя бы в следующем виде:
«Всякое материальное тело обладает свойством инерции, удерживающим его в состоянии покоя или равномерного прямолинейного движения. Сила, приложенная к телу для изменения этого состояния, испытывает сопротивление инерции тела, пропорциональное его массе.»
Однако, для доходчивости разъяснения Ньютон применил не совсем удачные с современной точки зрения термины «сила инерции» и «врождённая сила материи», введённые им с применением слова «сила», хотя из текста ясно, что на самом деле речь идёт о «врождённом СВОЙСТВЕ материи (массы)», а не силе, поскольку сила есть ВЕКТОР, обладающий направлением действия в пространстве, а вот «СВОЙСТВО ИНЕРЦИИ МАТЕРИИ (МАССЫ)» направлением не обладает и является величиной скалярной, а не векторной, и появляется во втором законе в виде скалярного множителя, обратно пропорционального величине массы тела, при пересчёте вектора воздействующей силы в вектор ускорения, вызванный этой силой и совпадающий по направлению с вектором действия силы. Как видим, свойство инертности массы тела является врождённым, скрытым от глаз и проявляющимся ТОЛЬКО в виде сопротивления при воздействии разгоняющей по скорости силы, или в виде напора при попытке замедлить скорость движения тела силой. Конечно же, Ньютон всё это прекрасно знал, но, видимо из удобства объяснения принятого в те времена применил термин «сила» вместо «свойство массы».
И если во времена Ньютона термин «сила» был вполне уместен для объяснения физики явления, то позднее, ситуация резко осложнилась после ввода в рассмотрение (для задач статики вместо динамики движении) Д’Аламбером и Эйлером разнообразных ФИКТИВНЫХ «СИЛ ИНЕРЦИИ» (для удобства расчётов в статике) путём как ОБМЕНА (ЗАМЕНЫ) РЕАЛЬНОГО УСКОРЕННОГО ДВИЖЕНИЯ тела НА ФИКТИВНУЮ СИЛУ, ПРИВОДЯЩУЮ К СТАТИЧНОЙ КАРТИНКЕ СО ВЗАИМНО УРАВНОВЕШЕННЫМИ СИЛАМИ, так и за счёт введения разных видов ФИКТИВНЫХ «СИЛ ИНЕРЦИИ», получаемых весьма простым путём формального умножения разных видов фиктивных ускорений движения тела в неинерциальных системах отсчёта на массу тела, что в соответствии со вторым законом равноценно появлению НОВЫХ фиктивных сил (со знаком минус перед ускорением!), действующих на тело, каких как «центробежные силы инерции», «кориолисова сила инерции» и т.п. За счёт таких ФИКТИВНИХ «СИЛ ИНЕРЦИИ» свойство инерции тела многие стали ошибочно отождествлять с этими силами, что по сути неправильно. Вспомним, что сам Ньютон применил термин «сила инерции», хотя это был синоним реального свойства тела сопротивляться воздействию приложенной к нему силы, а вовсе не фиктивная сила, введённая позже в неинерциальных системах вышеназванными учёными.
Этим тут же воспользоваись «любители реальности» фиктивных «сил инерции» в неинерциальных системах (см. критику книги А.А.Астахова в предыдущем комментарии), ссылаясь на вышерассмотренные термины «врождённая сила материи» и «сила инерции» у Ньютона в «Началах». На самом деле инерция тела проявляется не в виде ВЕКТОРНОЙ ФИКТИВНОЙ «СИЛЫ ИНЕРЦИИ», а в виде скалярного свойства ВЕЛИЧИНЫ МАССЫ тела, входящей во второй закон Ньютона при определении ускорения тела под воздействием результирующей силы, приложенной к телу для изменения его прежнего состояния. Многие забывают, что эти фиктивные «силы инерции» являются вторичными, не самостоятельными, а лишь являющимися ответной реакцией на активные центростремительное и переносное ускорения точек условного вращающегося твёрдого тела, которые ЧИСТО ВИЗУАЛЬНО приписываются от совпавшей в данный момент точки условного вращающегося твёрдого тела с рассматриваемым свободным телом БЕЗ РЕАЛЬНОГО ПРИЛОЖЕНИЯ К НЕМУ ПРИ ЭТОМ КАКИХ-ЛИБО СИЛ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ и поэтому их и надо просто ВЫЧЕСТЬ (т.е .прибавить со знаком МИНУС в виде уже фиктивных «антиускорений») из реального ускорения тела, рассчитанного под воздействием результирующей всех РЕАЛЬНЫХ сил приложенных к рассматриваемому телу для получений правильных расчётов динамики движения тела, а не умножать фиктивные ускорения на массу тела и плодить эти фиктивные силы в виде разных несуществующих «сил инерции».
В итоге, дело дошло до того, что многие поверили в РЕАЛЬНОСТЬ всех этих фиктивных «сил инерции», например, вполне серьёзно пытаются использовать фиктивную несуществующую центробежную силу для перемещения тела в направлении её действия от центра вращения, забывая о том, что это не самостоятельная сила, а лишь ответная реакция на центростремительную силу и стоит только убрать центростремительную силу, как, например, при раскручивании ядра легкоатлетом, то мгновенно пропадёт и центробежная сила как вторичная реакция вместе с центростремительной, а ядро полетит отнюдь не по радиусу вращения (как бы в направлении действия центробежной силы), а по нормали к радиусу вращения, т.е. по касательной к круговой траектории при одновременном пропадании обеих сил (центростремительной и как следствие пропадание центробежной) с накопленной окружной скоростью на момент отпускания ядра легкоатлетом.
Второй закон Ньютона
Этот центральный закон для расчёта динамики движения тел позволяет рассчитать величину ускорения движения тела при воздействии на него равнодействующей всех сил с учётом свойства инерции тела в виде его МАССЫ (описанного в первом Законе Ньютона), а затем и определить за счёт операции интегрирования проекций ускорения центра масс тела на оси выбранной системы отсчёта сначала составляющие проекций скорости, а за счёт интегрирования скоростей вычислить координаты, т.е. определить траекторию тела под воздействием равнодействующей всех сил, действующих на тело.
Эта задача расчёта динамики движения тела и была впервые сформулирована Ньютоном в «Началах» так же, как и обратная ей задача по определению ВЕЛИЧИНЫ результирующей силы, под действием которой сформировалась уже известная траектория движения тела, решаемая за счёт применения двойного дифференцирования траектории тела по времени.
Под силой в механике понимают всякую причину, изменяющую скорость тела.
Эти уравнения выведены при условии, что масса тела является постоянной величиной и независящей от скорости тела.
m * (dv/dt) = F; или, в другом виде: (dv/dt) = F / m; ……. (2.1)
m * (d2r/dt2) = F; или, в другом виде: (d2r/dt2 ) = F / m; ……. (2.2)
Величина F называется результирующей (геометрической суммой всех сил по правилу параллелограмма) силой, действующей на рассматриваемую материальную точку. Очевидно, что сила F является вектором (обладает направлением в пространстве), поскольку она равна производной вектора скорости по времени, или же второй производной от координаты тела.
Таким образом, в инерциальной системе отсчета производная от скорости (или ускорение) равна действующей на неё результирующей силе, отнесённой к массе тела. Это утверждение называется вторым законом Ньютона, а соответствующие ему уравнения — уравнениями движения материальной точки.
Прямое отношение ко второму Закону имеет Определение IV Ньютона о силах:
«Приложенная сила есть действие, производимое над телом, что бы изменить его состояние покоя или равномерного прямолинейного движения.»
Сила проявляется единственно только в действии, и по прекращении действия в теле не остаётся. Тело продолжает затем удерживать своё новое состояние вследствие одной только инерции. Происхождение приложенной силы может быть различное: от удара, от давления, от центростремительной силы.»
Кстати, в своих «Началах» Ньютон спокойно обошёлся без введения особых понятий об инерциальных и неинерциальных системах отсчёта, рассматривая лишь абсолютные и относительные движения материального тела, призывая лишь чётко разделять «истинные и кажущиеся движения»!
В связи общепринятым в учебниках принятым подчёркиванием необходимости обязательного наличия инерциальной системы для правильного выполнения второго закона. И даже такими , на мой взгляд, оскорбительными заявлениями о его якобы неработоспособности и неприменимости в неинерциальных системах, унижающими универсальность второго закона, хотелось бы просто сказать этим «интерпретаторам закона», что лучше бы они почитали «Начала» Ньютона, тогда может быть и поняли, что он все эти «проблемы второго закона» в неинерциальных системах отлично всё видел и призывал различать движение абсолютное и относительное (под коим он и понимал движение в неинерциальных системах), т.е. чётко видеть ускорения реальные (возникающие под воздействием реальных сил приложенных к рассматриваемому телу) и фиктивные (приписываемые телу без реального воздействия сил на него). Из-за отсутствия термина «ускорения» Ньютон их называл «истинные и кажущиеся движения». Давайте лучше почитаем самого Ньютона:
«Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения. Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется.»
Как же ещё лучше и яснее можно было сообщить авторам учебников о том, для его грамотного применения в неинерциальных системах второго закона необходимо чётко ВИДЕТЬ И ОТДЕЛЯТЬ от «истинного движения ( от действия сил, приложенных непосредственно к самому движущемуся телу)» «кажущиеся движения (которое может быть и произведено, и изменено без приложения сил к этому телу (когда для этого достаточно того, чтобы силы были приложены к телам, по отношению к которым это движение определяется)».
Что мы, в итоге, и делаем при рассмотрении «сложного движения» в теоретической механике, вычитая из правой части второго закона все эти реальные ускорения условного вращающегося тела («по отношению к которому это движение определяется») уже в качестве «кажущихся ускорений» («антицентростремительного», «антипереносного» и «антикорилисова» ускорений), чисто визуально и без всякого на то основания приписываемых рассматриваемому свободному телу, на самом деле не имеющему никакой физической наложенной связи с этой произвольно вращающейся системой (в виде условного вращающегося твёрдого тела вместе с его осями неинерциальной системы). Так что Ньютон весьма недвусмысленно распространил область действия второго закона и на неинерциальные системы (относительные в его терминологии) и поэтому не надо писать о «неработоспособности второго закона в неинерциальных системах», а надо лишь правильно учесть в нём все виды фиктивных отрицательных «антиускорений», освобождающих свободное тело в неинерциальных системах от приписываемых ему реальных ускорений условного вращающегося твёрдого тела неинерциальной системы, как о том и писал Ньютон.
Так же не надо делать и неграмотных выводов о том, что первый закон якобы излишен и вытекает как частный случай из второго закона при нулевой величине равнодействующей силы, приложенной к телу, подразумевая этим его ненужность и избыточность при наличии второго закона. Надо просто понять, что ПЕРВЫЙ ЗАКОН ПРЕЖДЕ ВСЕГО ПОСТУЛИРУЕТ «ВРОЖДЁННОЕ СВОЙСТВО ЛЮБОГО МАТЕРИАЛЬНОГО ТЕЛА ОБЛАДАТЬ ИНЕРЦИЕЙ, ПРОПОРЦИОНАЛЬНОЙ ВЕЛИЧИНЕ МАССЫ ТЕЛА, приводящей к стремлению тела сохранять своё постоянное прямолинейное движение (или состояние покоя).
Поэтому в неинерциальной системе во втором законе необходимо из реального ускорения тела, возникшего под воздействием суммы всех реальных сил (гравитационных сил притяжения, и, например, силы тяги двигателя, аэродинамических боковых сил управления и силы сопротивления при наличии атмосферы и т.п.) вычесть сразу все фиктивные «антиускорения», незаслуженно приписанные свободному телу без всякого реального воздействия на него соответствующих сил и вызванные визуальным наложением собственного вращения и (или) ускоренного движения неинерциальной системы относительно свободного тела.
Кроме того надо иметь в виду, что к активным реальным силам могут быть добавлены силы, появляющиеся при наложении на свободное тело физических связей с вращающейся системой, как-то, например, сила трения при контакте тела (без проскальзывания) с поверхностью сообщит свободному телу все реальные ускорения вращающейся поверхности, и в частности, реальную «Силу Кориолиса» со знаком плюс перед кориолисовым ускорением (не путать с уже учтённым выше «антикориолисовым» ускорением со знаком минус), возникающая при наличии относительной скорости перемещения по вращающейся поверхности
В итоге будут получены значения во времени проекций относительного ускорения тела в неинерциальной системе, первый и второй интегралы от которых и позволят определить проекции скорости и координаты траектории (с учётом начальных условий по скорости и координатам тела).
Таким образом и решается, поставленная самим Ньютоном, задача расчёта динамики материального тела в классической механике с применением второго закона Ньютона независимо от применяемой системы отсчёта с обязательной необходимостью учёта особенностей появления ускорений формально приписываемых телу за счёт неинерционности системы отсчёта и которые необходимо вычитать в виде "антиускорений" из реального ускорения тела, полученного в результате воздействия на него равнодействующей всех реальных сил.
Третий закон Ньютона – Закон появления сил от взаимодействия тел.
В современной трактовке третий закон в учебниках формулиуется обычно следующим образом:
Силы взаимодействия двух материальных точек равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.
При этом все забывают отметить расширенную трактовку Ньютоном всего многообразия возможных воздействий, сводя его лишь к давлению одного тела на другое. Первый и третий законы описывают два важных понятия в механике: свойство инерции тела в виде его массы и возможные источники появления самих сил, определеющие величину ускорения тела во втором законе механики. Авторство третьего закона признаётся бесспорным за самим Ньютоном и никем не оспаривалось.
Ньютон писал в «Началах» о всех возможных источниках появления силы:
« Происхождение приложенной силы может быть различное: от удара, от давления, от центростремительной силы.»
Поэтому у Ньютона, в отличие от современной трактовки его закона, смысл Третьего закона гораздо шире по видам взаимодействия между телами и он рассматривает ВСЕ ВОЗМОЖНЫЕ ВИДЫ ПОЯВЛЕНИЯ ПАРНЫХ СИЛ ЗА СЧЁТ ВЗАИМОДЕЙСТВИЯ ДВУХ МАТЕРИАЛЬНЫХ ТЕЛ и в нём идёт речь не только о равенстве сил при контакте двух взаимодействующих сил («от давления»), но и об обмене количеством движения между двумя взаимодействующими телами, например, как "при ударе тел" и даже с учётом их собственного вращения (см. теорию удара вращающихся тел в физике), а так же на расстоянии («от центростремительной силы») за счёт равных сил гравитационного притяжения в соответствии с законом взаимного притяжения («обратных квадратов»).
Вот изложение третьего закона у Ньютона с пояснениями к нему:
«Действию всегда есть равное противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.»
Если какое-нибудь тело, ударившись о другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своём собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга постоянно равны. От таких взаимодействий всегда происходят равные изменения не скоростей, а количеств движения, предполагая, конечно, что тела никаким другим усилиям не подвергаются. Изменения скоростей, происходящие также в противоположные стороны, будут пропорциональны массам тел, ибо количества движения получают равные изменения. Этот закон имеет место и для притяжений».
Рассмотрим подробнее это третий закон «для притяжений», исходя из того, что количество движения системы, состоящей, например, из двух тел равно произведению ПОЛНОЙ МАССЫ системы на СКОРОСТЬ ЕЁ ЦЕНТРА ИНЕРЦИИ, следует, что:
Q = m1 · V1 + m2 · V2 = (m1 + m2) · Vцентра системы = 0; (примем, например, что Vцентра системы =0)
И для неподвижного центра инерции двух тел получаем, что
m1 · V1 = - m2 · V2 , равенство количества движения относительно барцентра … (3.1)
что означает РАВЕНСТВО количества движения у двух взаимодействующих тел ОТНОСИТЕЛЬНО ИХ ОБЩЕГО ЦЕНТРА ИНЕРЦИИ (МАСС), знак минус свидетельствует о противоположной направленности векторов скоростей этих тел при их вращении вокруг общего центра инерции, который часто называют ещё и барцентром вращения взаимно притягивающичся тел. А поскольку вектора двух в каждый момент времени строго противоположны друг другу, то это означает, что тела вращаются с одной и той же угловой скоростью вращения ω относительно барцентра в противоположные стороны, поэтому можно заменить орбитальные скорости на выр.:
V1 = ω ·r1 и V2 = ω ·r2 , после их подстановки в выр. 3.1 и сокращения на скорость ω получим выр.(3.2) для моментов массы тел относительно барцентра, представляющие собой просто равенство моментов масс тела, равное обычному правилу моментов сил для рычага (для этого лишь достаточно умножить на одно и тоже значение гравитационного притяжения из закона взаимного притяжения (обратных квадратов) для этой пары тел):
m1 · r1 = - m2 · r2 ; равенство моментов массы относительно барцентра ……….(3.2)
Вы видите какие важные следствия вытекают из полной трактовки третьего закона для космических взаимно притягивающихся тел, позволяющие определить параметры их общего центра вращения (или центра инерции), т.е. барцентра, в котором и следует располагать начало систем координат для исследования движения взаимно притягивающихся космических тел, поскольку сам барцентр движется равномерно и прямолинейно или покоится, что существенно упрощает все выражения для ускорений движения рассматриваемых тел во втором законе.
На этом данная тема практически исчерпана.
P.S. Следующая, видимо не очень скорая, публикация будет посвящена светлой памяти RMR-astra, предложившей обратить внимание на тему рассмотрения устойчивости движения в либрационных точках Лагранжа (L1-L5). Возможно, будет создана и программа для расчёта пространственного движения тел в неинерциальной системе «Солнце - планета» для определения траекторий движения космических тел не только в областях, близким к либрационным точкам, но и для расчёта пролётных траекторий опасных для планеты астероидов.
Однако, до свидания и берегите себя от вирусов.
Георгий. 28.03.2020г. 22час.50мин. Время моск.
Уважаемый Георгий!
Интересный экскурс в историю физики. Спасибо!
Но поскольку вы анонсировали еще и современный взгляд на законы Ньютона, сделаю небольшое дополнение. Хотя сам Ньютон свой закон формулировал в форме $F=ma$, сейчас такой подход следует считать неточным. Дело в том, что закон должен отражать некоторую экспериментальную закономерность с уже определенными величинами. Однако сила $F$ как количественная характеристика некоторого физического фактора так или иначе опять связана со вторым законом Ньютона. Вы специально этому посвятили несколько разделов для определения силы. Поэтому более правильная формулировка второго закона Ньютона должна выглядеть так. "Отношение ускорений различных тел, помещенных в одну и ту же физическую обстановку, относятся друг к другу, как обратное отношение их масс". Другими словами:
$$
\frac{a_1}{a_2}=\frac{m_2}{m_1},~~\frac{a_2}{a_3}=\frac{m_3}{m_2}, ~~\frac{a_1}{a_3}=\frac{m_3}{m_1},\cdots
$$
Отсюда:
$$
m_1a_1=m_2a_2=m_3a_3=\cdots=F
$$
Величина $F$, однозначно характеризующая воздействие физической обстановки на тела, называется силой. Ускорение $a$ является чисто геометрической величиной, не требующей дополнительного определения. Масса $m$ - некоторый параметр, характеризующий количество вещества. Теперь становится ясно, что сила $F$ - есть физический фактор, вытекающий из второго закона Ньютона. Задача физики - это выяснение того, как $F$ связана с физической обстановкой.
Я здесь не стал уточнять, что ускорение и сила являются векторами. Это очевидное расширение закона. Есть еще одно расширение, связанное с тем, что само тело может изменять физическую обстановку. Так обстоят дела в законе Всемирного тяготения и законе Кулона, например. В этих законах сила, вызывающая ускорение, зависит от массы или заряда самого тела. Однако в этом случае второй закон Ньютона должен формулироваться для пробных тел (с бесконечно малыми массами и зарядами), что обеспечиваает сушествование напряженностей полей. Это дает более точное понимание того, с чем мы имеем дело в теории тяготения и электродинамике. Это же сразу высвечивает трудности этих теорий. На макромасштабах проблем нет. Но в микромире и массы, и заряды частиц, таких как электроны, протоны и т.д., не могут иметь массу и заряд меньше определенной величины. Минимальная масса электрона - масса покоя, а заряд всегда кратен заряду электрона. Поэтому на этом уровне второй закон Ньютона уже не может рассматриваться как фундаментальный. Но это уже другая история.
Уважаемый zhvictorm!
Прочитав впечатляющий список Ваших публикаций понял, что у Вас есть научные работы по теории гравитации. А меня как раз очень волнуют и интересуют вопросы реального подтверждения физическими опытами наличия гравитации между телами малой массы. С планетами всё ясно. А вот, есть ли у Вас ссылки на реальные современные данные, причём подробные, с реальными цифрами эксперимента (а не итоговые общие выводы), например, полученные на современных крутильных весах типа опыта Кавендиша по сериям опытов (с периодами колебаний весов, что меня в первую очередь и интересует, если, конечно, такие современные установки ещё существуют). Или данные других современных опытов, реально подверждающих наличие гравитации между телами с массами гораздо меньшими, чем у планет. А то меня как-то не устраивают отсылки на результаты опытов многовековой давности и всё равно без конкретных данных по измерениям. Где найти данные о фактических измерениях с применением современной техники, или это тоже "военная тайна", как и многое другое, скрываемое от общественности? Как-то наткнулся на описание современного опыта по измерению притяжения даже между атомами при их вертикальном падении в закрытом объёме, а вот чем всё это закончилось - незвестно.
В основе сомнений лежит, конечно же, статья некоего А.А.Гришаева (О.Х.Деревенский - это его псевдоним), сомневающегося в наличии гравитации между малыми телами.(http://newfiz.info/gra-opus.htm). После прочтения которой не поленился создать программу моделирования опыта Кавендиша со всеми размерами и массами его установки. В итоге получил данные о том, что при переводе притягивающих шаров из дальнего состояния в ближнее период колебания крутильных весов для установки Кавендиша должен увеличиваться почти ровно в ДВА РАЗА. Как, известно, но углу отклонения весов измерить притяжение не получается из-за малозатухающего колебательного поведения весов с периодом колебания до десятков минут. Так вот мои попытки найти подтверждающие аналогичные РЕАЛЬНЫЕ данные экспериментов на современных крутильных весах в интернете ни к чему не привели.
Как бы Вы кратко возразили А,А,Гришаеву, хотя бы просто ссылками на реальные измерения, а не на общие выводы типа "есть и точка"?
Георгий. 23.03.2020г 22с55м.Время моск.
Уважаемый Георгий!
Постараюсь ответить на ваш вопрос. Эксперименты по измерению гравитационной постоянной проводятся до сих пор в разных странах. Эксперимент типа Кавендиша проводился, по крайней мере, лет десять-пятнадцать назад у нас где-то в Подмосковье. Такие эксперименты проводились в Китае, США и других странах. Вот пару ссылок на информацию об этих экспериментах:
1. Новые измерения гравитационной постоянной еще сильнее запутывают ситуацию
2. Гравитационная постоянная измерена новыми методами
В этих экспериментах измерения проводились для малых по массе телах, когда их массу можно точно контролировать. Проблема состоит в том, что разброс измерений оказывается слишком большим от эксперимента к эксперименту. Он чаще всего превышает приборную погрешность самих экспериментов. Доверительные интервалы не пересекаются. На следующей картинке (взятой из работы [ссылка 1] ) это показано очень наглядно:
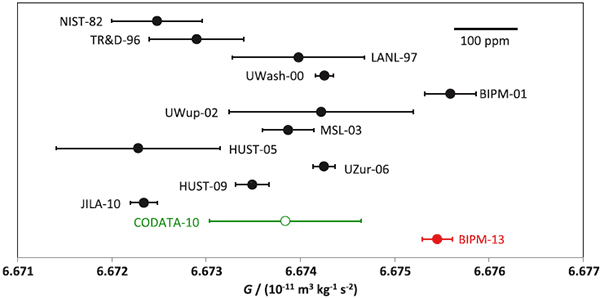
Это данные на 2013 год. К настоящему времени ситуация, насколько я знаю, не изменилась существенно. Подробности смотрите в [ссылка 1]. Это означает, что мы чего-то не знаем важного по поводу этой силы.
У меня на этот счет своя теория. Она изложена в моих работах по теории частиц. На сайте их можно найти. Другие предполагают, что дело в существовании дополнительной пятой силы. Но как видно из всевозможных экспериментов сила тяготения есть, и примерно такая, как это дается теорией тяготения Ньютона. Величина несколько меняется от каких-то не контролируемых условий эксперимента, но существует во всех экспериментах.
Кроме этого, есть гигантский набор астрономических наблюдений, который подтверждает наличие этой силы для газа и пыли, распределенных на пространстве в тысячи световых лет и больше. Друго дело, что концы с концами часто не сходятся. Это в первую очередь касается "темной материи". Большинство физиков и астрофизиков считают, что это некий тип материи. Эту материю ищут уже лет пятьдесят, а то и больше, но найти не могут. По моим представлениям, это изменение формы закона тяготения на больших масштабах, которые мы воспринимаем как дополнительную массу. Причем изменения формы тяготения не такие, как предсказывает ОТО. Но это, как говорится, другая история.
Уважаемый zhvictorm!
Большое спасибо, что нашли время ответить на мою просьбу. Книгу Милюкова и Сагитова мне уже доводилось ранее читать как одну из немногих популярных на тему определения гравитации. А вот в Вашей новой ссылке обнаружил что-то мне не очень понятный отказ от измерения периода колебания крутильных весов и это при малозатухающих колебаниях с их перерегулированием! Как можно что-то тогда определить, по величине заброса что ли? Или они умудрились ввести неплохое демпфирующее усилие, гасящее перерегулирование. Изменение периода ведь понадёжнее будет. Не очень понятно. Главное, видимо,что притяжение между малыми массами всё-таки, видимо, есть (для меня это самое важное), если столько разных групп работает над этим вопросом. Просто мне хотелось сравнить, например, свои расчёты и экспериментальные данные в виде графика колебания маятника. Но видимо, не судьба. Кстати, на мой взгляд, неоправданно привлекать какие-либо виды электростатических полей, какими бы благими намерениями ни оправдывалось их введение, что бы случайно не перепутать их между собой, имеющими одинаковую обратно квадратическую зависимость. Ибо уже появились сторонники электростатической версии поисхождения силы гравитационного притяжения между телами.
Кстати, где-то читал, что сама сила гравитации не очень стабильна и слегка изменяется на больших промежутках времени (месяцы и годы), что , видимо и не позволяет добиться стабильности в измерениях. Все измерения на разных установках желательно было бы договориться проводить разным группам исследователей одновременно, что бы исключить этот неизвестный фактор влияния, видимо, из далёкого космоса, а может быть и не очень далёкого, а от Солнца. Неплохо было бы привлечь одновременный учёт результатов измерений гравитации Солнца по данным проекта "Паркер", если они , конечно, предусмотрены этой программой.
Ещё раз спасибо за информацию.
Георгий. 28.03.2020 23ч45м Время моск.