7. Метод функциональных подстановок. Новые подходы
7.1. Многофункциональные подстановки
7.1.1. Введение
Среди методов построения и анализа точных решений нелинейных уравнений в частных производных, используемых в прикладных физических задачах, особую роль играет метод обратной задачи (МОЗ), имеющий несколько вариантов своего использования. Наиболее важными из них являются метод обратной задачи рассеяния [TSol,Dod] и метод преобразований Дарбу [M79,MS91,MS90]. Параллельно с МОЗ существует метод функциональных подстановок (МФП), который, вообще говоря, возник значительно раньше, чем МОЗ, но долгое время существовал в форме лишь нескольких несвязанных между собой результатов, наиболее важным из которых являлся результат Коула-Хопфа [Hopf,Cole], относящийся к уравнению Бюргерса [Burg74]. В 80-х годах прошлого века в результате развития МОЗ была обнаружена некоторая общность между уравнениями, линеаризуемыми с помощью подстановок типа Коула-Хопфа и МОЗ [Sv85]-[San92]. Уравнения, интегрируемые с помощью подстановок Коула-Хопфа, впоследствии были названы уравнениями типа Бюргерса и составили достаточно широкий класс интегрируемых уравнений. В работах [ZhN07,ZhZ08-1,ZhZ08-2,ZhTMF09] был предложен метод, позволяющий строить уравнения типа Бюргерса и их решения с помощью обобщенных подстановок типа Коула-Хопфа. Этот метод может быть применен к целому ряду прикладных задач, в частности, к задачам гидродинамики сжимаемой жидкости [ZhZ08-1,ZhZ08-2] и некоторым другим задачам [ZhTMF09,ZhND14,ZhSTFI18].
Метод строится на основе анализа условий совместности некоторой базовой системы линейных уравнений. В отличие от метода обратной задачи предлагаемый метод опирается не на сами условия совместности, а на дифференциальные следствия исходной системы уравнений. Как показано в [ZhN07,ZhZ08-1,ZhZ08-2,ZhTMF09,ZhND14], эту совокупность базовых дифференциальных соотношений всегда можно дополнить еще одним уравнением, замыкающим систему нелинейных уравнений типа Бюргерса. Свойства построенных таким образом уравнений типа Бюргерса определяются типом вспомогательного уравнения. Например, полная интегрируемость построенного уравнения связана с интегрируемостью вспомогательного уравнения, при этом последнее может быть и нелинейным [ZhZ08-1,ZhZ08-2].
В работе [ZhIZVP18] был получен предварительный результат, состоящий в том, что между методом МФП и МОЗ существует связь, прослеженная в этих работах на примере нелинейного уравнения Шредингера (НУШ) для односолитонных его решений. Связь достигается рассмотрением дополнительного вспомогательного уравнения. Однако в случае многосолитонных решений связь явно не просматривается в силу того, что в стандартном МФП нет возможности строить решения, содержащие несколько линейно независимых функций, удовлетворяющих некоторым линейным уравнениям, что является одним из элементов МОЗ, например, в форме метода преобразований Дарбу. В настоящей работе развивается подход, основанный на расширении метода МФП, который связан с многофункциональными подстановками, которые воспроизводят в расширенном виде особенности процедуры одевания операторов в рамках МОЗ, основанного на преобразованиях Дарбу [M79,MS91]. В работе сначала описывается общая взаимосвязь методов МФП и МОЗ в форме метода преобразований Дарбу с представлением диаграммы соответствия между уравнениями этих методов. Затем строится общая процедура построения многофункциональных подстановок и приводятся примеры ее использования для уравнений Кортевега-де Вриза (КдВ) и НУШ.
7.1.2. Матричные функциональные подстановки
Метод МФП [ZhN07,ZhTMF09] в размерности 1+1 строится на основе двух исходных соотношений, называемых базовыми, для одной вспомогательной матричной функции $\hat{T(x,t)}$ произвольной матричной размерности $n\times n$, с элементами, зависящими от двух независимых переменных $x$ и $t$. Базовые соотношения могут иметь множество различных, но эквивалентных форм [ZhN07,ZhTMF09]. Выбор той или иной формы определяется в первую очередь тем, что эти базовые соотношения позволяют однозначно связать вспомогательную функцию ${\hat T}(x,t)$ с набором функциональных параметров, которые и удовлетворяют искомым нелинейным интегрируемым уравнениям. Простейшей формой базовых соотношений являются соотношения первого порядка: $${\hat T}_x={\hat A}{\hat T},~~{\hat T}_{t}={\hat B}{\hat T},\tag{1.1}\label{EqBase}$$ где ${\hat A}$ и ${\hat B}(x,t)$ - комплексные матричные функции той же размерности $n\times n$, элементы которых будем называть коэффициентами базовых соотношений. Если функция ${\hat T}(x,t)$ задана, то функциональные параметры ${\hat A}(x,t)$ и ${\hat B}(x,t)$ однозначно выражаются через саму функцию ${\hat T}$ и ее производные: $${\hat A}={\hat T}_x{\hat T}^{-1},\quad{\hat B}={\hat T}_{t}{\hat T}^{-1},\tag{1.2}\label{DefSubAB}$$ что можно рассматривать как дифференциальные подстановки типа Коула-Хопфа.
С другой стороны, требование, что функция ${\hat T}(x,t)$ одновременно обращает в тождество два уравнения (\ref{EqBase}), накладывает на функции ${\hat A}(x,t)$ и ${\hat B}(x,t)$ ограничение, которое можно выразить в форме одного матричного уравнения: $${\hat A}_t-{\hat B}_x+[{\hat A},{\hat B}]=0,\tag{1.3}\label{EqStr1}$$ совпадающего по форме с уравнением Захарова-Шабата в теории МОЗ, но имеющее несколько иной смысл, поскольку не содержит в явном виде спектрального параметра.
При выполнении (\ref{EqStr1}) все производные функции ${\hat T}$ можно выразить через саму функцию ${\hat T}$: $${\hat T}^{[n,k]} = \frac{\partial^{n+k}}{\partial x^n\partial t^k}{\hat T} = {\hat A}^{[n,k]}{\hat T},$$ где матричные функции ${\hat A}^{[n,k]}$ могут быть вычислены рекуррентно по формулам: $${\hat A}^{[n+1,k]}={\hat A}^{[n,k]}_x + {\hat A}^{[n,k]}{\hat A},$$ $${\hat A}^{[n,k+1]}={\hat A}^{[n,k]}_t + {\hat A}^{[n,k]}{\hat B},\quad k=0,1,\ldots,\tag{1.4}\label{EqRec}$$ с начальными условиями: $${\hat A}^{[1,0]} ={\hat A},\quad{\hat A}^{[0,1]} ={\hat B}.$$
К базовой системе (\ref{EqBase}) можно добавить произвольное интегрируемое уравнение для ${\hat T}$. В качестве такого интегрируемого уравнения проще всего использовать линейное уравнение с постоянными коэффициентами ${\hat C}_{n,k}$ конечного порядка $L$: $$\sum\limits_{k=0}^{L}\sum\limits_{k+n=0}^{L}{\hat C}_{n,k}{\hat T}^{[n,k]}=0.\tag{1.5}\label{EqIntT}$$ Эти уравнения, называемые в дальнейшем вспомогательными, в итоге, после исключения из соотношений (\ref{DefSubAB}) и (\ref{EqRec}) всех производных функции ${\hat T}$ и самой функции, превращаются в нелинейные уравнения относительно элементов матричных функций ${\hat A},\ {\hat B}$: $$\sum\limits_{k=0}^{L}\sum\limits_{k+n=1}^{L}{\hat C}_{n,k}{\hat A}^{[n,k]}+{\hat C}_{00}=0.\tag{1.6}\label{EqABadd}$$ Вспомогательное уравнение в форме (\ref{EqABadd}) вместе с уравнением (\ref{EqStr1}) и системой равенств (\ref{EqRec}) образует замкнутую систему относительно элементов двух функций ${\hat A},\ {\hat B}$.
Такой подход, представляющий собой МФП, в дальнейшем будем называть методом функциональных подстановок первого порядка. Примеры нелинейных уравнений, которые получаются с помощью соответствующих подстановок в методе МФП, приведены в [ZhTMF09]. Результаты применения различных вариантов такого подхода можно найти в работах [ZhZ08-1,ZhZ08-2,ZhND14,ZhSTFI18,ZhIZVP18].
7.1.3. Функциональные подстановки второго порядка
Основной принцип видоизменений схемы МФП, предлагаемый в данной работе, продемонстрируем сначала на примере простой их формы, связанной с введением трех вспомогательных матричных функций размерности $n\times n$, вместо одной в стандартной схеме МФП, кратко изложенной выше.
$${\hat T}_{xx}={\hat a}_0(x,t){\hat T}+{\hat a}_1(x,t){\hat T}_x+{\hat a}_2(x,t){\hat T}_t,$$ $${\hat T}_{xt}={\hat b}_0(x,t){\hat T}+{\hat b}_1(x,t){\hat T}_x+{\hat b}_2(x,t){\hat T}_t,\tag{1.7}\label{EqBT2m}$$ $${\hat T}_{tt}={\hat c}_0(x,t){\hat T}+{\hat c}_1(x,t){\hat T}_x+{\hat c}_2(x,t){\hat T}_t.$$ По порядку производных в левой части данную систему будем называть базовой системой второго порядка. В таком подходе число коэффициентов базовых соотношений равно девяти. Для задания всех коэффициентов этой системы требуется задать три линейно независимые матричные функции ${\hat T}_1,{\hat T}_2,{\hat T}_3$. В результате систему базовых соотношений можно записать в форме матричного равенства: $$\hat{F}_3 = \widehat{R}_3 \widehat{\Psi}_3,\tag{1.8}\label{DefBaseR}$$ где введены обозначения: $$\widehat{\Psi}_3 =\left(\begin{array}{ccc} {\hat T}_1 & {\hat T}_2 & {\hat T}_3 \\ {\hat T}_{1,x} & {\hat T}_{2,x} & {\hat T}_{3,x} \\ {\hat T}_{1,t} & {\hat T}_{2,t} & {\hat T}_{3,t} \end{array}\right),~\widehat{R}_3=\left(\begin{array}{ccc} {\hat a}_0 & {\hat a}_1 & {\hat a}_2 \\ {\hat b}_0 & {\hat b}_1 & {\hat b}_2 \\ {\hat c}_0 & {\hat c}_1 & {\hat c}_2 \end{array}\right),~\widehat{F}_3 = \left(\begin{array}{ccc} {\hat T}_{1,xx} & {\hat T}_{2,xx} & {\hat T}_{3,xx} \\ {\hat T}_{1,xt} & {\hat T}_{2,xt} & {\hat T}_{3,xt} \\ {\hat T}_{1,tt} & {\hat T}_{2,tt} & {\hat T}_{3,tt} \end{array}\right).\tag{1.9}\label{DefPsi3}$$
Если матрица $\widehat{\Psi}_3$ не вырождена, то элементы матрицы $\widehat{R}_3$ вычисляются однозначно из матричного соотношения: $$\widehat{R}_3=\widehat{F}_3\widehat{\Psi}_3^{-1}.$$
Систему базовых уравнений (\ref{EqBT2m}) можно представить в виде пары матричных уравнений следующего вида: $$\frac{\partial}{\partial x}\left(\begin{array}{l} \hat{T} \\ \hat{T}_x \\ \hat{T}_t\end{array}\right)=
\left(\begin{array}{lll} \hat{O} & \hat{I} & \hat{O}\\ \hat{a}_0 & \hat{a}_1 & \hat{a}_2 \\ \hat{b}_0 & \hat{b}_1 & \hat{b}_2\end{array}\right)\left(\begin{array}{l} \hat{T} \\ \hat{T}_x \\
\hat{T}_t\end{array}\right)=\hat{A}_3\left(\begin{array}{l} \hat{T} \\ \hat{T}_x \\
\hat{T}_t\end{array}\right),\tag{1.10}\label{EqMBT2m}$$ $$\frac{\partial}{\partial t}\left(\begin{array}{l} \hat{T} \\ \hat{T}_x \\
\hat{T}_t\end{array}\right)=\left(\begin{array}{lll} \hat{O} & \hat{O} & \hat{I} \\ \hat{b}_0 & \hat{b}_1 & \hat{b}_2 \\ \hat{c}_0 &
\hat{c}_1 & \hat{c}_2\end{array}\right)\left(\begin{array}{l} \hat{T} \\ \hat{T}_x \\ \hat{T}_t\end{array}\right)=\hat{B}_3\left(\begin{array}{l} \hat{T} \\ \hat{T}_x \\
\hat{T}_t\end{array}\right).$$ Здесь $\hat{O}$ - матрица со всеми нулевыми элементами, а $\hat{I}$ - единичная матрица размерности $n\times n$.
Система (\ref{EqMBT2m}) получена из (\ref{EqBT2m}) с помощью дополнения ее двумя формальными тождествами: $$\frac{\partial}{\partial x}\hat{T} = \hat{T}_x,\quad \frac{\partial}{\partial t}\hat{T} = \hat{T}_t,$$ которые содержатся в первых строках матриц $\hat{A}_3$ и $\hat{B}_3$ общей размерности $3n\times 3n$. $$\frac{\partial}{\partial x}\widehat{\Psi}_{3}=\hat{A}_3\widehat{\Psi}_{3},\quad \frac{\partial}{\partial t}\widehat{\Psi}_{3}=\hat{B}_3\widehat{\Psi}_{3},\tag{1.11}\label{EqBM2}$$ Опять по построению эта система совместна. Поэтому, если функциональные параметры базовой системы вычисляются из (\ref{EqBT2m}) при заданных функциях $\hat{T}_1,~\hat{T}_2,~\hat{T}_3$ (при условии ${\rm det}\hat{\Psi}_2\not\equiv 0$), то для матриц $\hat{A}_3$ и $\hat{B}_3$ выполняется матричное тождество: $$\Big(\frac{\partial}{\partial t}\hat{A}_3-\frac{\partial}{\partial x}\hat{B}_3+[\hat{A}_3,\hat{B}_3]\Big)\widehat{\Psi}_{3}=0.\tag{1.12}\label{EqUV2}$$ Эта система уравнений приводится к шести матричным уравнениям, имеющим вид: $$\hat{a}_{0,t}-\hat{b}_{0,x}+(\hat{a}_1-\hat{b}_2)\hat{b}_0+\hat{a}_2\hat{c}_0-\hat{b}_1\hat{a}_0 = 0,$$ $$\hat{a}_{1,t}-\hat{b}_{1,x}+\hat{a}_2\hat{c}_1-\hat{b}_2\hat{b}_1+[\hat{a}_1,\hat{b}_1]-\hat{b}_0 = 0,$$ $$\hat{a}_{2,t}-\hat{b}_{2,x}-\hat{b}_1\hat{a}_2+\hat{a}_2\hat{c}_2+(\hat{a}_1-\hat{b}_2)\hat{b}_2+\hat{a}_0 =0,\tag{1.13}\label{EqSys2m}$$ $$\hat{b}_{0,t}-\hat{c}_{0,x}+\hat{b}_1\hat{b}_0+\hat{b}_2\hat{c}_0-\hat{c}_1\hat{a}_0-\hat{c}_2\hat{b}_0 =0,$$ $$\hat{b}_{1,t}-\hat{c}_{1,x}+(\hat{b}_1-\hat{c}_2)\hat{b}_1+\hat{b}_2\hat{c}_1-\hat{c}_1\hat{a}_1-\hat{c}_0 =0,$$ $$\hat{b}_{2,t}-\hat{c}_{2,x}-\hat{c}_1\hat{a}_2+\hat{b}_1\hat{b}_2+[\hat{b}_2,\hat{c}_2]+\hat{b}_0=0.$$
Эта система содержит шесть матричных уравнений для девяти коэффициентов базовых соотношений и является не замкнутой. В соответствии с общей идеологией МФП, если ${\hat T}_i$ выбирать из множества решений уравнений определенного типа, то к системе уравнений (\ref{EqSys2m}) добавляются уравнения на коэффициенты базовых соотношений, которые замыкают эту систему.
В качестве примера рассмотрим вспомогательное уравнение в форме уравнения теплопроводности, аналогичные тем, которые используются для вывода уравнения Бюргерса в схеме МФП [ZhTMF09]: $$\hat{T}_{i,xx}=\lambda \hat{T}_i + u_0 \hat{T}_{i,x}+ \varepsilon {\hat T}_{i,t},\quad i=1,2,3,\tag{1.14}\label{EqT012}$$ где $u_0,\varepsilon,\lambda$ - некоторые вещественные постоянные. Сравнивая эти соотношения с базовыми (\ref{EqBT2m}), находим: ${\hat a}_0=\lambda$, ${\hat a}_1=u_0={\rm const}$, ${\hat a}_2=\varepsilon={\rm const}$. В результате для функций $\hat{b}_1,~\hat{b}_2,~\hat{b}_3$ получаем замкнутую систему: $$\varepsilon\hat{b}_{0,t}-\hat{b}_{0,xx}-2\hat{b}_{2,x}\hat{b}_0-u_0\hat{b}_{0,x}-2\lambda\hat{b}_{1,x}=0,$$ $$\varepsilon \hat{b}_{1,t}-\hat{b}_{1,xx}-2\hat{b}_{2,x}\hat{b}_1-u_0\hat{b}_{1,x}-2\hat{b}_{0,x}=0,\tag{1.15}\label{Eqbb012}$$ $$\varepsilon\hat{b}_{2,t}-\hat{b}_{2,xx}-2\hat{b}_{2,x}\hat{b}_2-u_0\hat{b}_{2,x}-2\hat{b}_{1,x}=0.$$ и систему соотношений для функций $\hat{c}_0,\hat{c}_1,\hat{c}_2$: $$\hat{c}_0=\varepsilon^{-1}\Big[\hat{b}_{0,x}+\hat{b}_{2}\hat{b}_{0}+\lambda\hat{b}_{1}-u_0\hat{b}_{2}\hat{b}_{1}\Big],$$ $$\hat{c}_1=\varepsilon^{-1}\Big[\hat{b}_{1,x}+\hat{b}_{2}\hat{b}_{1}+\hat{b}_{0}\Big],$$ $$\hat{c}_2=\varepsilon^{-1}\Big[\hat{b}_{2,x}+\hat{b}^2_{2}-\lambda \hat{I}+\lambda\hat{b}_{1}-u_0\hat{b}_{2}\Big].$$ Уравнения (\ref{Eqbb012}) представляют собой систему уравнений, обобщающую уравнение Бюргерса.
7.1.4. Дополнительные вспомогательные соотношения и уравнение КдВ
Согласно общей идее, которая была первоначально продемонстрирована в [ZhIZVP18] на примере НУШ, получения посредством подстановок решения уравнений, интегрируемых с помощью МОЗ, в общую схему замыкания базовой системы необходимо включить дополнительные вспомогательные уравнения. В качестве основного примера реализации такого подхода рассмотрим ее применение для построения многосолитонных решений уравнений КдВ. Рассмотрим систему базовых соотношений \rf{EqBT2m} со скалярными функциями $T_i(x,t),~i=1,2,3$, которые удовлетворяют системе вспомогательных уравнений следующего вида: $$T_{i,xxx}=T_{i,t},\quad T_{i,xx}=\lambda_i T_i,~~i=1,\ldots,3,\tag{1.16}\label{EqTT}$$ где $\lambda_i,~i=1,2,3$ - некоторые постоянные. Каждая функция $T_i$ теперь удовлетворяет паре уравнений и, поэтому, выбирается из более ограниченного класса решений, чем в рассмотренном выше случае с уравнением теплопроводности. Важным является то, что оба типа вспомогательных уравнений можно, исключив из них основные функции $T_i$, представить в виде дополнительных уравнений для коэффициентов $a_i,b_i,c_i$ базовых соотношений. Эти дополнительные уравнения позволяют, не меняя вида решений, заданных базовыми соотношениями, существенно расширить множество уравнений, которым удовлетворяют коэффициенты базовых соотношений [ZhIZVP18]. В результате, среди этого множества уравнений будут содержаться и уравнения, интегрируемые с помощью МОЗ. В случае (\ref{EqTT}) - это уравнение КдВ.
Соотношения (\ref{EqTT}) генерируют дополнительные к (\ref{EqUV2}) соотношения для элементов матриц $\hat{A}_3$ и $\hat{B}_3$, определенных в (\ref{EqMBT2m}). Дифференцируя (\ref{EqMBT2m}) по $x$, находим: $$\frac{\partial^2}{\partial x^2}\widehat{\Psi}_3=\left[\hat{A}_{3,x}+\hat{A}_3^2\right]\widehat{\Psi}_3=\widehat{U}_3\widehat{\Psi}_3=\widehat{\Psi}_3\widehat{L},\tag{1.17}\label{EqD3Psi}$$ $$\frac{\partial^3}{\partial x^3}\widehat{\Psi}_3=\left[\hat{A}_{3,xx}+2\hat{A}_{3,x}\hat{A}_3+\hat{A}_3\hat{A}_{3,x}+\hat{A}_3^3\right]\widehat{\Psi}_3= \hat{B}_3\widehat{\Psi}_3,\tag{1.18}\label{EqD2Psi}$$ где матрица $\widehat{\Psi}_3$ определена в (\ref{DefPsi3}), а матрицы $\hat{U}_3$ и $\hat{L}$ такие: $$\hat{U}_3=\left(\begin{array}{ccc} a_0 & a_1 & a_2\\ 0 & 0 & 1\\ B_0 & B_1 & B_2 \end{array}\right),~~\hat{L}=\left(\begin{array}{ccc}\lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array}\right).$$ Здесь: $$ B_0 = a_{0,t}+a_1b_0+a_2c_0,~~B_1 = a_{1,t}+a_1b_1+a_0+ a_2c_1,$$ $$B_2 = a_{2,t}+a_1b_2+a_2c_2+a_0,$$ $$\hat{B}_3=\hat{A}_{3,xx}+2\hat{A}_{3,x}\hat{A}_3+\hat{A}_3\hat{A}_{3,x}+\hat{A}_3^3.$$
Подставляя это соотношение в (\ref{EqUV2}), приходим к матричному уравнению: $$\hat{A}_{3,t}-\hat{A}_{3,xxx}-\frac{\partial}{\partial x}\Big[2\hat{A}_{3,x}\hat{A}_3+\hat{A}_3\hat{A}_{3,x}+\hat{A}_3^3\Big]+$$ $$+[\hat{A}_3,\hat{A}_{3,xx}]+2[\hat{A}_3,\hat{A}_{3,x}]\hat{A}_3+\hat{A}_3[\hat{A}_3,\hat{A}_{3,x}]=0.\tag{1.19}\label{EqA3}$$ Чтобы в покомпонентной записи этих уравнений содержалось уравнение КдВ, к нему необходимо добавить условия, вытекающие из (\ref{EqD2Psi}). Для того, чтобы из этих условий исключить матрицу $\hat{L}_3$, их можно записать в таком виде: $$\frac{\partial}{\partial x}\hat{U}_3+[\hat{U}_3,\hat{A}_3]=0,\quad \frac{\partial}{\partial t}\hat{U}_3+[\hat{U}_3,\hat{B}_3]=0.\tag{1.20}\label{EqUA2}$$ Проблема состоит в том, что изначально неясно, какой именно коэффициент базовых соотношений (или их комбинация) удовлетворяют уравнению КдВ. Все остальные коэффициенты будут удовлетворять уравнениям других типов. Чтобы решить эту проблему, воспользуемся сравнением базовых соотношений с уравнениями для определения коэффициентов одевающего оператора в методе преобразований Дарбу в МОЗ [M79,MS90,Zh02M] для КдВ.
7.1.5. Метод сравнения с преобразованиями Дарбу для уравнения КдВ
Уравнение КдВ: $$u_t+\frac{3}{2}uu_x-\frac{1}{4}u_{xxx}=0,\tag{1.21}\label{EqKdV}$$ имеет представление Лакса в форме условия коммутативности операторов: $$\hat{L}=\frac{\partial^2}{\partial x^2}-u(x,t),~~\hat{A}=\frac{\partial}{\partial t}-\frac{\partial^3}{\partial x^3}+\frac{3}{2}u(x,t)\frac{\partial}{\partial x}+\frac{3}{4}u_x(x,t).$$ Для построения точных решений этого уравнения можно применить метод преобразований Дарбу [MS90,MS91]. Преобразование Дарбу для уравнений КдВ строится как процедура ``одевания голых'' операторов: $$\hat{A}_0=\frac{\partial}{\partial t}-\frac{\partial^3}{\partial x^3},~~\hat{L}_0=\frac{\partial^2}{\partial x^2}.$$
Для одевания рассматривается линейный оператор $\hat{M}_N$ следующего вида: $$\hat{M}_N=\frac{\partial^N}{\partial x^N}+\xi_N(x,t)\frac{\partial^{N-1}}{\partial x^{N-1}}+\ldots+\xi_{0}(x,t).\tag{1.22}\label{DefMND}$$ Для того, чтобы операторы $\hat{A}_0$, $\hat{L}_0$ и $\hat{M}_N$ обладали $N$ общими собственными функциями необходимо и достаточно, чтобы существовали операторы $\hat{D}_A$ и $\hat{D}_L$ такие, что: $$[\hat{A}_0,\hat{M}_N]=\hat{D}_A\hat{M}_N,\quad [\hat{L}_0,\hat{M}_N]=\hat{D}_L\hat{M}_N.\tag{1.23}\label{DefCom}$$ Выполнения этих условий можно добиться явным заданием $N$ функций $\psi_k,~k=1,\cdots,N$, которые одновременно удовлетворяют следующей системе уравнений: $$\hat{A}_0\psi_k=\frac{\partial}{\partial t}\psi_k-\frac{\partial^3}{\partial x^3}\psi_k=0, \quad\hat{L}_0\psi_k=\frac{\partial^2}{\partial x^2}\psi_k=\lambda_k\psi_k,\quad k=1,\ldots,N,\tag{1.24}\label{Eqpsi}$$ при условии, что все они являются собственными функциями оператора $\hat{M}_N$, отвечающими его нулевому собственному значению: $$\hat{M}_K\psi_k=\left[\frac{\partial^K}{\partial x^K}+\xi_K(x,t)\frac{\partial^{K-1}}{\partial x^{K-1}}+\ldots+\xi_{0}(x,t)\right]\psi_k=0,
\quad k=1,\ldots,K.\tag{1.25}\label{EqMpsi}$$ Последние $K$ уравнений можно рассматривать как неоднородную линейную алгебраическую систему $K$ уравнений относительно $K$ коэффициентов $\xi_{k},~k=0,\ldots,K-1$, которая имеет единственное решение при условии линейной независимости функций $\psi_k$. Согласно указанной теореме операторы $\hat{D}_A$ и $\hat{D}_L$ существуют, а их явный вид можно вычислить, непосредственно вычисляя коммутаторы в правых частях операторных уравнений \rf{DefCom}. В частности, имеем: $$\hat{D}_L= u(x,t), \quad\hat{D}_A=-\frac{3}{2}u\frac{\partial}{\partial x}-\frac{3}{4}u_x,$$ где $u(x,t)$ имеет вид: $$u(x,t)=2\xi_{N-1,x}.\tag{1.26}\label{SolKdV}$$ В результате можно показать, что операторы: $$\hat{A}_1 = \hat{A}_0 -\hat{D}_A=\frac{\partial}{\partial t}-\frac{\partial^3}{\partial x^3}+\frac{3}{2}u\frac{\partial}{\partial x}+\frac{3}{4}u_x,$$ $$\hat{L}_1=\hat{L}_0-\hat{D}_L=\frac{\partial^2}{\partial x^2}-u(x,t),\tag{1.27}\label{EqOp}$$ коммутируют между собой, т.е. обладают полным набором общих собственных функций $\phi(x,t,\lambda)$, имеющих вид: $$\phi(x,t,\lambda)=\hat{M}_K\psi(x,t,\lambda),$$ где $\psi(x,t,\lambda)$ удовлетворяют уравнениям: $$\hat{A}_0\psi(x,t,\lambda)=0,\quad \hat{L}_0\psi(x,t,\lambda)=\lambda\psi(x,t,\lambda),$$ для любого комплексного значения спектрального параметра $\lambda$. Вычисляя коммутатор операторов $\hat{A}_1$ и $\hat{L}_1$, находим: $$[\hat{A}_1,\hat{L}_1]=-\Big(u_t-\frac{3}{2}uu_x-\frac{1}{4}u_{xxx}\Big)=0,$$ т.е. функция $u(x,t)$ удовлетворяет уравнению КдВ (\ref{EqKdV}). Сравнивая соотношения (\ref{Eqpsi}) с (\ref{EqTT}), видим их полную идентичность при условии, что $K=3$ и равенствах $\psi_i=T_i,~i=1,2,3$. При этом базовые соотношения (\ref{EqBT2m}) необходимо сравнить с уравнениями (\ref{EqMpsi}) на собственные функции одевающего оператора Дарбу, с помощью которых вычисляются коэффициенты, соответственно, базовых соотношений и коэффициенты $\xi_i$ одевающего оператора $\hat{M}_3$. Первое уравнение из \ref{EqBT2m}, заменяя в нем производные $T_{k,t}$ на производные $T_{k,xxx}$, можно записать в следующем виде: $$T_{k,xxx}-\frac{1}{a_2}T_{k,xx}+\frac{a_1}{a_2}T_{k,x}+\frac{a_0}{a_2}T_{k}=0,\tag{1.28}\label{EqTk}\quad k=1,2,3.$$ что в точности совпадает с (\ref{EqMpsi}) при выполнении условий: $$\xi_2=-\frac{1}{a_2},\quad\xi_1=\frac{a_1}{a_2},\quad\xi_0=\frac{a_0}{a_2}.$$ Отсюда следует $\xi_2=-a_2^{-1}$. Поэтому функция $$u(x,t)= 2\xi_{2,x}=2\frac{a_{2,x}}{a_2^2},\tag{1.29}\label{SolKdV3}$$ удовлетворяет уравнению КдВ в соответствии с методом преобразований Дарбу, изложенному выше. Поэтому решения, которые получаются с помощью подстановок второго порядка для уравнения КдВ, представляют собой 3-солитонные (квазисолитонные) решения этого уравнения.
Оставшиеся два уравнения системы базовых соотношений (\ref{EqBT2m}) после замены $T_{k,t}$ на $T_{k,xxx}$ выглядят так: $$T_{k,xxxx}-b_2 T_{k,xxx}-b_1T_{k,x}-b_0T_{k}=0,$$ $$T_{k,xxxxxx}-c_2 T_{k,xxx}-c_1T_{k,x}-c_0T_{k}=0,\quad k=1,2,3.\tag{1.30}\label{DefMd3}$$
Можно видеть, что формально, операторы порядка $4$ и $6$, соответствующие этим уравнениям, также можно рассматривать как одевающие операторы для уравнений, которым удовлетворяют коэффициенты этих операторов. Число ненулевых коэффициентов этих операторов равно трем. Cледовательно, из условия того, что функции $T_k$ являются их собственными функциями, отвечающими нулевому собственному значению, полностью определяют их коэффициенты $b_i(x,t)$ и $c_i(x,t)$.
7.2. Метод функциональных подстановок в задачах физической и биологической кинетики
В работе [ZhZhKNS] было развито расширение метода функциональных подстановок (МФП) на случай уравнений с обобщенными производными, в том числе с производными, определенными на дискретных сетках, например, разностных производных. Такой подход позволяет перенести ряд результатов, имеющих место для уравнений в частных производных [ZhTMF09], на случай дискретных динамических систем. Дискретные динамические системы играют важную роль в различных разделах механики, теории конденсированного состояния вещества и математической биологии.
Среди всех дискретных динамических систем особую роль играют дискретные цепочки уравнений, важным примером которых являются интегрируемые цепочки Тоды, Ленгмюра и т.д. [Toda,BM03]. Цепочки Тоды и некоторые другие цепочки такого типа интегрируются с помощью метода обратной задачи (МОЗ) [BM03,Scott]. Одним из наиболее важных приложениий дискретных цепочек являются модели взаимодействующих между собой атомарных и молекулярных цепочек [BM03,Scott]. Однако системы в виде дискретных цепочек более общих элементов находят применение и в хими и биологии [Scott].
Построение интегрируемых моделей типа дискретных цепочек с помощью МФП вляется альтернативой к МОЗ, расширяющей число примеров интегрируемых моделей такого рода. Такие модели обладают более широким набором свойств. В данной работе излагаются результаты применения МФП к задачам построения и интегрирования уравнений типа дискретных цепочек. Общая идеология предлагаемого подхода опирается на работы [ZhTMF09,ZhZhKNS], но реализуется на более простой схеме базовых соотношений.
7.2.1. Линейные операторы на сетках
Динамика дискретных автономных бесконечномерных и конечномерных нелинейных динамических систем формально может быть связана с системами обыкновенных дифференицальных уравнений первого порядка: $$\frac{d{\bf x}}{dt}={\bf F}({\bf x}),\tag{2.1}\label{DefNDSys}$$ где ${\bf x}=\{\ldots,x_{i-1}(t),x_i(t),x_{i+1}(t)\ldots\}$, $i=(-\infty,\infty)$ - вектор координат динамической системы, а ${\bf F}=\{\ldots,F_{i-1}({\bf x}),F_i({\bf x}),F_{i+1({\bf x})}\ldots\}$ - некоторые заданные функции, зависящие от ${\bf x}$. Вместе с нелинейными системами (\ref{DefNDSys}) будем рассматривать и вспомогательные линейные динамические системы: $$\frac{d {\bf p}}{dt}=\hat{{\bf M}}{\bf p},\tag{2.2}\label{DefNDSys1}$$ где ${\bf p}=\{\ldots,\phi_{i-1}(t),\phi_i(t),\phi_{i+1}(t)\ldots\}$ и $\hat{{\bf M}}$ - бесконечно-мерная матрица с постоянными коэффиценты. Отметим, что на ряду с бесконечно-мерными динамическими системами будут рассмаьтриваться и кончномерные, для которых вектора ${\bf x}$ и ${\bf p}$, а также матрица $\hat{{\bf M}}$ будут конечными, нумерация элементов которых будет начинаться от 0. В частности: ${\bf x}=\{x_0(t),\ldots,x_n(t)\}$, ${\bf p}=\{\phi_0(t),\ldots,\phi_n(t)\}$, где $n$ - размерность динамической системы.
Метод функциональных подстановок опирается на систему базовых соотношений, которые в наиболее простом виде таковы: $${\hat D}_x Φ=AΦ,\quad\hat{D}_t Φ=BΦ,\tag{2.3}\label{EqBAB}$$, где $Φ$ - функция, заданная на двумерном пространстве $R^2=X\times T$ с координатами $x$ и $t$. В данной работе будем полагать, что время $t$ является непрерывным, а координата $x$ - дискретной. Последнее означает, что значения функции $Φ(x,t)$ представлены значениями $Φ_i(t),\ i\in(-\infty,\infty)$ в узлах сетки $x_i,i\in(-\infty,\infty)$ вдоль координаты $x$ с равноотстоящими узлами с шагом $h_x$. Оператор $\hat{D}_t$ в данной работе будет представлять собой обыкновенную производную по t: $$\hat{D}_t\equiv\frac{\partial}{\partial t}$$. Оператор $\hat{D}_x$ будет представлять собой некоторую сеточную производную, определенную в узлах $x_i$ сетки.
Рассмотрим следующие типы производных. Это сдвиговые производные (s-производные) вперед и назад: $$\hat{{\bf D}}_+ \Phi_i(t) = \Phi_{i+1}(t),\quad\hat{{\bf D}}_- \Phi_i(t) = \Phi_{i-1}(t), $$ Сеточные производные в форме левой $\hat{{\bf D}}_L$ и правой $\hat{{\bf D}}_R$ конечных разностей (далее h-производные) выражаются через операторы сдвига с помощью соотношений: $$\hat{{\bf D}}_L \Phi_i(t)=\frac{1}{h_x}\Big(\Phi_{i+1}-\Phi_{i}\Big)=\frac{1}{h_x}(\hat{{\bf D}}_+-1)\Phi_i,$$ $$\hat{{\bf D}}_R \Phi_i(t)=\frac{1}{h_x}\Big(\Phi_{i}-\Phi_{i-1}\Big)=-\frac{1}{h_x}(\hat{{\bf D}}_- -1)\Phi_i.$$ Поэтому в дальнейшем можно ограничится рассмотрением только сдвиговых производных.
7.2.2. Базовые соотношения для сеточных производных
Для s-произвордных по отдельности правила Лейбница выполняются в следующей форме:
$$\hat{{\bf D}}_{+}(A_i\Phi_i)=A_{i+1}\Phi_{i+1}=\hat{{\bf D}}_+A_{i}\hat{{\bf D}}_+\Phi_{i},$$ $$\hat{{\bf D}}_{-}(A_i\Phi_i)=A_{i-1}\Phi_{i-1}=\hat{{\bf D}}_-A_{i}\hat{{\bf D}}_- \Phi_{i},$$ Связь между производными вперед и назад определяется очевидным тождеством: $$\hat{{\bf D}}_{+}\hat{{\bf D}}_{-}\Phi_i=\hat{{\bf D}}_{-}\hat{{\bf D}}_{+}\Phi_i=\Phi_i. \tag{2.4}\label{DefDpm}$$ Поскольку для сеточных уравнений необходимо рассматривать две координатные производные (вперед и назад), то базовые соотношения (\ref{EqBAB}) должны быть расширены. В данной работе эти соотношения имеют такой вид: $$\hat{{\bf D}}_+ \Phi_i = A_i(t)\Phi_i,\quad \hat{{\bf D}}_- \Phi_i = B_i(t)\Phi_i,\quad\frac{\partial}{\partial t} \Phi_i = C_i(t)\Phi_i,\tag{2.5}\label{DefBaseN},$$ где $A_i(t),B_i(t),C_i(t)$ - базовые сеточные функии. Далее функцию $\Phi_i(t)$ будем называть основной.
При заданной функции $\Phi_i(t)$ базовые функции $A_i(t)$ и $B_i(t)$ вычисляются из базовых соотношений. При этом базовые функции оказываются связанными соотношением, которое не зависит от вида основной функции $\Phi_i(t)$. Действительно, не трудно проверить, что все введенные операторы сеточных производных $\hat{{\bf D}}_x$ и непрерывная производная по $t$ $\hat{{\bf D}}_t$ коммутирую между собой. Например, для сдвиговой левой производной имеем: $$(\hat{{\bf D}}_+\hat{{\bf D}}_t-\hat{{\bf D}}_t\hat{{\bf D}}_+)\Phi_i=\frac{\partial \Phi_{i+1}}{\partial t }-\frac{\partial \Phi_{i+1}}{\partial t }\equiv 0,$$ аналогично и для остальных типов производных. Исходя из этого, находим условия связи между базовыми функциями $A_i$ и $B_i$ для s-производных: $$(\hat{{\bf D}}_+\hat{{\bf D}}_t-\hat{{\bf D}}_t\hat{{\bf D}}_+)\Phi_i=\hat{{\bf D}}_+(B_i\Phi_i)-\hat{{\bf D}}_t(A_i\Phi_i)=$$ $$=B_{i+1}\Phi_{i+1}-\frac{\partial A_i}{\partial t}\Phi_i-A_{i}\frac{\partial \Phi_i}{\partial t}
=\Big(\Big(C_{i+1}-C_i\Big)A_i-\frac{\partial A_i}{\partial t}\Big)\Phi_i=0.$$ По аналогии отсюда находим: $$\frac{\partial A_i}{\partial t}=\Big(C_{i+1}-C_i\Big)A_i,\quad\frac{\partial B_i}{\partial t}=\Big(C_{i-1}-C_{i}\Big)B_i.\tag{1.26}\label{EqCompABS}$$
К этим соотношениям связи необходимо добавить следствия из тождеств (\ref{DefDpm}), которые после использования базовых соотношений приобретают такой вид: $$B_{i+1}A_i=A_{i-1}B_i=1,$$ откуда следует связь между функциями $A_i$ и $B_i$: $$B_{i}=\frac{1}{A_{i-1}}.\tag{2.8}\label{ConAB}$$
7.2.3. Рекуррентные соотношения для старших производных
Поскольку базовые соотношения и соотношения связи между функциями $A_i$ и $B_i$ выполняются для любой функции $\Phi_i$, то имеется возможность установить вид ограничений, которые возникают, когда функции $\Phi_i(t)$ выбираются из множества решений некотрого конкретного интегрируемого уравнения не обязательно линейного. Такое уравнение в дальнейшем будем именовать вспомогательным. В случае, если вспомогательное уравнение после подстановки в него базовых соотношений допускает исключение из него основной функции $\Phi_i$, полученное уравнение дает еще одну дополнительную связь между функциями $A_i$ и $B_i$. Для вычисления высших производных, которые могут содержать вспомгательные уравнения по обеим переменным, полезно воспользоваться рекуррентными соотношениями, вытекающими непосредственно из базовых соотношений. Введем обозначения: $$\frac{\partial^m}{\partial t^m}{\hat{\bf D}}_x^k\Phi_i = A^{[k,m]}_i(t)\Phi_i.\tag{2.8}\label{EqDiff}$$ Здесь $A_i^{[k,m]}(t)$ вычисляются с помощью рекуррентных соотношений: $$A^{[k+1,m]}_i=A^{[k,m]}_{i+1}A_{i},\quad A^{[k,m+1]}_i=\frac{\partial}{\partial t}A^{[k,m]}_{i}+A^{[k,m]}_{i}B_{i},$$ $$A^{[1,0]}_{i}=A_i,\quad A^{[0,1]}_{i}=B_i,\quad k=0,1,2\ldots,~~m=0,1,2,\ldots.\tag{2.9}\label{EqBaseRecS}$$ Заметим, что первое рекуррентное соотношение приводит следующему представлению для $A^{[k+1,0]}_i$: $$A^{[k+1,0]}_i=\prod_{j=0}^{k}A_{i+j}=A_{i+k}A_{i+k-1}\cdots A_{i}.\tag{2.10}\label{DefAk0}$$
7.2.4. Вычисление уравнений нелинейных цепочек
В качестве вспомогательного уравнения для основной функции $\Phi_i$ рассмотрим линейное уравнение следующего общего вида: $$\frac{\partial}{\partial t}\Phi_i=\sum\limits_{k=0}^nM_k\hat{{\bf D}}_x^k \Phi_i, \tag{2.11}\label{EqPhin}$$ где $n$ - натуральное число, $M_k(t)$ - в общем случае функции времени, а под $\hat{{\bf D}}_x$ понимается производная одного типа - либо левая, либо правая. Введем бесконечный вектор: ${\bf U}=\{\ldots,\Phi_0,\Phi_1,\Phi_2,\ldots\}$ и бесконечную матрицу $\hat{{\bf M}}$ со строками, содержащими одинаковые элементы $M_i,~i=0,\ldots,n$, но сдвинутыми на 1 вправо. В результате (\ref{EqPhin}) можно записать в общем виде так: $$\frac{d{\bf U}}{dt} =\hat{{\bf M}} {\bf U}.\tag{2.12}\label{EqUM}$$
Используя базовые соотношения (\ref{DefBaseN}) и (\ref{DefAk0}) для левой и правой s-производных, уравнение (\ref{EqPhin}) приводится к вспомогательным уравнениям связи: $$(\hat{{\bf D}}_+):\hspace{0.1cm} C_i=M_0+\sum\limits_{k=1}^n M_k\prod\limits_{p=0}^{k-1}A_{i+p},$$ $$(\hat{{\bf D}}_{-}):\hspace{0.1cm} C_i=M_0+\sum\limits_{k=1}^n M_k\prod\limits_{p=0}^{k-1}B_{i-p}.\tag{2.13}\label{DefBiS}$$ Подставляя $C_i$ из этого соотношения в уравнение связи (\ref{EqCompABS}), приходим к уравнению следующего вида: $$\frac{\partial}{\partial t}\ln A_{i}=\sum\limits_{k=1}^nM_k(A_{i+k}-A_i)\prod\limits_{p=1}^{k-1}A_{i+p}.\tag{2.14}\label{EqNtAn}$$ В частности, для $n=1,2,3$ имеем такое уравнение:$$\frac{\partial}{\partial t}\ln A_{i}=M_1(A_{i+1}-A_i)+M_2(A_{i+2}-A_i)A_{i+1}+M_3(A_{i+3}-A_i)A_{i+2}A_{i+1}.\tag{2.15}\label{EqNA3}$$
Структура уравнений (\ref{EqNtAn}) и (\ref{EqNA3}) подсказывает, что эти ураанения можно привести к форме, подобной цепочкам Тоды, с помощью экспоненциальных подстановок $A_i=e^{\phi_i}$ для $\hat{{\bf D}}_+$ и $A_i=(e^{\phi_i}-1)/h_x$. В этом случае уравнения (\ref{EqNtAn}) преобразуются к следующему виду: $$\frac{\partial}{\partial t}\phi_{i}=
\sum\limits_{k=1}^nM_k(e^{\phi_{i+k}}-e^{\phi_i})\exp\left\{\sum\limits_{p=1}^{k-1}\phi_{i+p}\right\}=R_{i+1}e^{\phi_{i+1}}-R_ie^{\phi_i},\tag{2.16}\label{EqEToda}$$ где:$$R_i=M_1+\sum\limits_{k=2}^nM_k\exp\left\{\sum\limits_{p=1}^{k-1}\phi_{i+p}\right\}.$$ В частном случае (\ref{EqNA3}) имеем: $$\frac{\partial}{\partial t}\phi_{i}=M_1(e^{\phi_{i+1}}-e^{\phi_i})+M_2(e^{\phi_{i+2}}-e^{\phi_i})e^{\phi_{i+1}}+M_3(e^{\phi_{i+3}}-e^{\phi_i})e^{\phi_{i+2}+\phi_{i+1}}.\tag{2.17}\label{EqLTphi3}$$ Аналогичные уравнения возникают и в случае использования $\hat{{\bf D}}_L$. В отличие от цепочек Тоды данные уравнения имеют первый порядок по времени и требуют отдельной интерпретации.
7.2.5. Уравнения с правой и левой производными первого порядка
Рассмотрим особый случай вспомогательных уравнений, содержащих левую и правую s-производные. Полная система уравнений связим ежду коэффициентами базовых соотношений $A_i,B_i,C_i$ имеют такой вид: $$\frac{\partial A_i}{\partial t}=A_i\Big(C_{i+1}-C_i\Big),$$ $$\frac{\partial B_i}{\partial t}=-B_i\Big(C_{i}-C_{i-1}\Big),\tag{2.18}\label{EqGABC}$$ $$B_{i+1}A_i-A_{i-1}B_i=0.$$ Последнее соотношение является условием коммутативности левой и правой s-производных. Введем вместо $A_i$ и $B_i$ новые функции в соответствие с правилами: $$A_i =e^{\psi_i},~~B_i =e^{\phi_i}.\tag{2.19}\label{Defpsiphi}$$ Тогда совокупность уравнений связи (\ref{EqGABC}) примет такой вид: $$\frac{\partial \psi_i}{\partial t}=C_{i+1}-C_i,\quad\frac{\partial \phi_i}{\partial t}=-\Big(C_{i}-C_{i-1}\Big),\quad\phi_{i+1}+\psi_i=\psi_{i-1}+\phi_i.\tag{2.20}\label{EqPABC}$$ К этим соотношениям следует добавить еще тождество: $$\psi_i+\phi_{i+1}=0,\tag{2.21}\label{ConPP}$$ вытекающее из третьего уравнения системы (\ref{EqGABC}).
Рассмотрим теперь вспомогательное уравнение следующего общего вида:$$\frac{\partial \Phi_i}{\partial t}=(M\hat{{\bf D}}_+ + N\hat{{\bf D}}_-+L_i)\Phi_i,\tag{2.22}\label{EqPQ1}$$ где $M$, $N$ и $L_i$ - некоторые, независящие от $t$ числа. Используя базовые соотношения (\ref{DefBaseN}) и соотношения (\ref{Defpsiphi}) и (\ref{ConPP}), преобразуем уравнение (\ref{EqPQ1}) к форме связи бзовых коэффициентов: $$C_i=MA_i+NB_i=Me^{\psi_i}+Ne^{\phi_i}+L_i.\tag{2.23}\label{EqCABC}$$ Подставляя это выражение в первое уравнение системы (\ref{EqPABC}) и используя (\ref{ConPP}), находим: $$\frac{\partial \psi_i}{\partial t}=M\Big(e^{\psi_{i+1}}-e^{\psi_i}\Big)+N\Big(e^{-\psi_i}-e^{-\psi_{i-1}}\Big)+I_i,\tag{2.24}\label{Eqpsi1}$$ где, как и раньше, $I_i=L_{i+1}-L_i$.
7.2.6. Интегралы движения
Построение решений рассмотренных бесконечных цепочек строится из решений линейных вспомогательных уравнений с помощью базовых соотношений, в частности, для всех типов вспомогательных уравнений, если найдены решения для $\Phi_i$, решения для $A_i,B_i,\phi_i$ можно представить в следующей форме: $$A_i=\Phi_{i+1}(t)/\Phi_i(t),~\phi_i=\ln A_i,~~B_i=\Phi_{i-1}/\Phi_i.\tag{2.27}\label{SolABphi}$$
Для общего анализа свойств рассмотренных динамических систем необходимо иметь возможность вычислять их интегралы движения. Эти интегралы для этих систем строятся с помощью интегралов движения системы (\ref{EqUM}). Обозначим через ${\bf v}_k=(\ldots,v^0_k,v^1_k,v^2_k,\ldots),~k\in[-\infty,\infty]$ - левые собственные вектора матрицы $\hat{{\bf M}}$, соотвествующие собственному числу $\lambda_k$, как в конечномерном, так и бесконечномерном случаях. Тогда, умножая (\ref{EqUM}) слева на ${\bf v}_k$, находим: $$\frac{d}{dt}V_k = \lambda_k V_k,~~V_k({\bf U})=({\bf v}_k,{\bf U})=\sum\limits_{a=-\infty}^{\infty}v_k^{a}\Phi_a.\tag{2.28}\label{EqVk}$$ Предположим,что среди всех собственных чисел $\lambda_k$ нет кратных. Пусть далее $\lambda_0\not= 0$ - отличное от нуля собственное число системы (\ref{EqUM}). В этом случае имеем: $$t=\frac{1}{\lambda_k}\ln V_k-H_k,$$ где $H_k$ - постоянные интегрирования.
Тогда интегралами системы (\ref{EqUM}) являются все возможные функции: $$I_{k}=H_k-H_0=\frac{1}{\mu_k}\ln V_k({\bf U})-\frac{1}{\mu_0}\ln V_0({\bf U}),~~k\not=0.\tag{2.29}\label{DefInt}$$ Для всех $k$, у которых $\lambda_k=0$ интегралами являются сами функции $V_k({\bf U})$. Обращая соотношения (\ref{SolABphi}), находим: $$\Phi_i =\Phi_0\prod\limits_{j=0}^{i-1}A_{j},~i>0,~\Phi_i = \Phi_0\prod\limits_{j=1}^{i}A^{-1}_{j},~i<0.$$ Отсюда $V_k=\Phi_0Q_k$, где: $$Q_k=v^0_k+\sum\limits_{a=1}^{\infty}\Big(v_k^{-a}\prod\limits_{j=1}^{a}A^{-1}_{j}+v_k^{a}\prod\limits_{j=1}^{a}A_{j}\Big).$$
Подставляя эти соотношения в (\ref{DefInt}) и исключая из нтегралов функцию $\ln\Phi_0(t)$, окончательно находим, что интегралами движения цепочек будут величины: $$J_{km}=\frac{\ln Q_k}{\lambda_0-\lambda_k}-\frac{\ln Q_m}{\lambda_0-\lambda_m}-\frac{(\lambda_k-\lambda_m)\ln Q_0}{(\lambda_0-\lambda_k)(\lambda_0-\lambda_m)},\tag{2.30}\label{DefJkm}$$ где $k\not=m\not= 0$. В эту схему аналогичным образом включаются и интегралы, соотвествующие нулевому собственнуму числу. Пусть для определенности $\lambda_0=0$.Тогда в последнем соотношении необходимо просто потребовать обращения в ноль $\lambda_0$.
Если среди собственных чисел имеются кратные собственные числа, то вычисление интегралов для этой группы проводится по нресколько другой схеме. Пусть, как и раньше, $\lambda_0\not=0$ - некоторое не кратное собственное число, и $\lambda_{p}=\lambda_{p+1}=\ldots =\lambda_{q}$, где $q>p$. В этом случае часть уравнений (\ref{EqUM}) с соответствующими номерами после умножения слева на ${\bf v}_k$ преобразуется к форме Жордана \cite{Belman69}. Исходя из этого, уравнения для функций $V_{k},k=p,\ldots,q$ в общем случае можно записать в такой форме:$$\dot{V}_k=\lambda_pV_k+V_{k+1},~~k=p,\ldots,q-1,~~\dot{V}_q=\lambda_pV_q.$$ Заметим, что если матрица $\hat{{\bf M}}$ является верхнетреугольной или нижнетреугольной, то матрицу не обязательно приводить к форме Жордана, а уравнения для $V_k$ можно получать непосредственно из решения самой исходной системы (\ref{EqUM}).
В случае представления Жордана находим, что решения для функций $V_k$ в соответствующем диапазоне номеров имеет такой вид: $$V_{p+k} = \sum\limits_{\alpha=0}^{k}\frac{C_{s-\alpha}}{(k-\alpha)!} t^{k-\alpha} e^{\lambda_p t},~k=p,\ldots,s.$$ где $s=q-p$, а $C_{\alpha}$ - постоянные интегрирования. Для функций $V_q=Q_q\Phi_0$ и $V_0=Q_0\Phi_0$ имеем два соотношения:$$t=\frac{1}{\lambda_p}\Big(\ln Q_q+\ln\Phi_0-\ln C_s\Big),~~t=\frac{1}{\lambda_0}\Big(\ln Q_0+ \ln\Phi_0- H_0\Big),$$
Исключая из них $\Phi_0$, находим: $$t=\frac{1}{\Delta}Z_p,~~Z_p=\ln (Q_p/Q_0)-H_{p0}$$ где $H_{p0}=\ln C_s-H_0$ и $\Delta=\lambda_p-\lambda_0$. Используя последнее соотношение, находим интегралы движения в следующей форме: $$J_{kp}=\ln \Big(C_{s-k}/C_s\Big) = \ln\Big(Q_{p+k}/Q_q\Big) - \sum\limits_{\alpha=0}^{k}\frac{C_{s-\alpha}}{\Delta^{k-\alpha}(k-\alpha)!}Z_p^{k-\alpha},$$ $$k=1,\ldots,s-1.\tag{2.31}\label{DefJLL}$$ Эти интегралы с заданным $k$ вычисляются рекуррентно через значения интегралов с $k-1$.
7.2.7. Циклические цепочки
Отдельный класс цепочек, связанных со сдвиговыми производными возникает, если дополнительно потребовать, что после конечного числа сдвигов базовые уравнения переходят сами в себя. Это условие можно выразить следующим соотношением: $$\hat{{\bf D}}_+\Phi_i =\Phi_{i+1},~\hat{{\bf D}}_+\Phi_{i+1}=\Phi_{i+2},\ldots,\hat{{\bf D}}_+^q\Phi_i=\hat{{\bf D}}_+\Phi_{i+q-1}=\Phi_{i+q}=\Phi_i,$$ где $q$ - некоторое натуральное число, большее 1: $q>1$. В этом случае на коэффиценты базовых соотношений накладываются дополнительные условия, сводящиеся к двум соотношениям: $$\prod\limits_{k=0}^{q-1}A_{i+k}=1,~~A_{i+q}=A_i,~~C_{i+q}=C_i.\tag{2.32}\label{EqCyclAB}$$ В результате подстановки $\phi_i=\ln A_i$ первое и второе из этих соотношений сводятся к формулам: $$\sum\limits_{k=0}^{q-1}\phi_{i+k}=0,~~\phi_{q}=\phi_0.\tag{2.33}\label{EqCyclp}$$ Условия цикличности приводят к некоторым модификациям цепочек. Цепочки (\ref{EqEToda}) в случае $n=q$ приволятся к следующему виду: $$\frac{d}{d t}\phi_{i}=\sum\limits_{k=1}^{q-1}M_k(e^{\phi_{i+k}}-e^{\phi_i})\exp\left\{\sum\limits_{p=1}^{k-1}\phi_{i+p}\right\},~i=1,\ldots,q,
\tag{2.34}\label{EqCLat}$$ где $q$ функций $\phi_i,~i=1,\ldots,q-1$ связаны соотношением (\ref{EqCyclp}). В силу цикличности цепочки только $q-2$ функций являются независмыми. Поэтому индекс $i$ пробегает конечный интервад значений $i=0,1,\ldots,q-2$. В частном случае $q=2$ соотношение (\ref{EqCyclp}) имеет такой вид: $$\phi_i+\phi_{i+1}=0,$$ что эквивалентно: $$\phi_1=-\phi_0.$$ В этом случае, поскольку $B_{2}=B_0$, уравнение (\ref{EqCLat}) примет вид одного уравнения: $$\frac{d}{d t}\phi_{0}=M_1(e^{-\phi_{0}}-e^{\phi_0})=-2M_1{\rm sh}(\phi_0),\tag{2.35}\label{EqC2}$$ для функции $\phi_0$. В случае же $q=3$ уравнение (\ref{EqCLat}) имеет такой вид: $$\phi_i+\phi_{i+1}+\phi_{i+2}=0,$$ что приводит к двум уравнениям для $\phi_0$ и $\phi_1$: $$\frac{d}{d t}\phi_{0}=(M_1-M_2e^{\phi_0})e^{\phi_{1}}-M_1e^{\phi_0}+M_2e^{-\phi_0},$$ $$\frac{d}{d t}\phi_{1}=(M_1e^{-\phi_1}-M_2)e^{-\phi_{0}}-M_1e^{\phi_1}+M_2e^{-\phi_1}.\tag{2.36}\label{EqCL3}$$
Если ввести обознаения $x=e^{\phi_0}$ и $y=e^{\phi_1}$, то уравнение (\ref{EqC2}) сводится к уравнению Ферхюльста: $$\dot{x}=2M_1(1-x^2)$$ Система же (\ref{EqCL3}) превращается в систему следующего вида: $$\dot{x}=(M_1-M_2x)xy-M_1x^2+M_2,$$ $$\dot{y}=(M_1-M_2y)x^{-1}-M_1y^2+M_2,\tag{2.37}\label{Eqxy}$$ которая, как и уравнение Ферхюльста, может иметь приложение в задачах популяционной динамики или теории химических реакций.
7.2.8. Ограниченные цепочки
Еще одним классом интегрируемых моделей рассмотренного типа являются ограниченные цепочки, длина которых определяется условием обращения в ноль функций $\phi_i$, начиная с некотрого номера $q>0$ для цепочек со сдвигом вперед (или $q<0$ для цепочек со сдвигом назад). В качестве примера приведем цепочки типа (\ref{EqNtAn}). Потребуем, чтобы начиная с некоторого конечного номера $q\le n$ выполнялись условия: $$\Phi_{q+i}=\Phi_q,~~i=1,2,\ldots.$$ Тогда все уравнения для функций $\Phi_{q+i},~i>1$ превращаются в одно и тоже уравнение вида: $$\dot{\Phi}_{q}=\Phi_{q}\sum\limits_{i=0}^nM_i.$$ Уравнения с номерами меньшими $q$ будут отличаться от этого исходного уравнения. В результате все функции $A_{q+i}=\Phi_{i+q+1}/\Phi_{i+q}=1,~i>0$ будут равны 1, а функции $\phi_{q+i}=\ln A_{q+i}=0,~i>0$ - нулю. В результате совокупность уравнений для всех функций $\phi_i$ с номерами $-p<i<q$, где $p\le 0$ -любое неотрицательное число, является замкнутой и описывает конечную цепочку уравнений вида (\ref{EqNtAn}). В качестве примера приведем уравнения следующей цепочки с $n=2, q=3,p=0$: $$\dot{\phi}_{0}=M_1(e^{\phi_1}-e^{\phi_0})+M_2(e^{\phi_2}-e^{\phi_0})e^{\phi_1},$$ $$\dot{\phi}_{1}=M_1(e^{\phi_2}-e^{\phi_1})+M_2(1-e^{\phi_1})e^{\phi_2},$$ $$\dot{\phi}_{2}=(M_1+M_2)(1-e^{\phi_2}),$$ Если перейти к переменным $x=e^{\phi_0},~y=e^{\phi_1},~z=e^{\phi_2}$, то эти уравнения примут такой вид: $$\dot{x}=M_1(y-x)x+M_2(z-x)xy,$$ $$\dot{y}=M_1(z-y)y+M_2y^2-M_2zy^2,\tag{2.38}\label{Eqxyz}$$ $$\dot{z}=(M_1+M_2)(1-z)z.$$ Эта система также может использоваться в моделях химических реакций и популяционной динамкие в биологии. Аналогичные уравнения имеют место и для конечных цепочек с правым сдвигом. Однако цепочки со сдвигами обоих типов требуют отдельного рассмотрения, что выходит за рамки данной работы.
7.2.9. Цепочки с условиями отражения
Рассмотренные способы ограничения длины цепочек с помощью условия цикличности и условия обрезания не применимы к цепочкам содержащим одновременно и правые и левые производные. В этом случае для ограничения длины цепочек можно воспользоваться условием отражения. Условие отражения продемонстрируем на следующем примере. Рассмотрим цепочку вида (\ref{Eqpsi1}) со всопомогательными уравнениями (\ref{EqPQ1}) при условии $I_i=0$. Потребуем, чтобы выполнялись следующие условия: $$\phi_i = - \phi_{-i},~~i=0,1,2,\ldots.\tag{2.39}\label{ConRf1}$$ Из этих условий следует, что $\phi_0=0$, что автоматически приводит к требованию $M=N$. Не трудно видеть, что в этом случае уравнения (\ref{Eqpsi1}) для $i<0$ переходят в уравнения для $i>0$. Действительно, при $i<0$ уравнения: $$\frac{d\psi_{-|i|}}{d t}=M\Big(e^{\psi_{-|i|+1}}-e^{\psi_{-|i|}}\Big)+M\Big(e^{-\psi_{-|i|}}-e^{-\psi_{-|i|-1}}\Big),$$ в силу условий отражения переходят в уравнения: $$ \frac{d \psi_{|i|}}{d t}=M\Big(e^{\psi_{-|i+1|}}-e^{-\psi_{|i|}}\Big)+M\Big(e^{\psi_{-|i|}}-e^{\psi_{-|i-1|}}\Big),$$ что в точности совпадает с уравнениями при $i>0$. Таким образом, можно получить полубесконечную цепочку. Условиям отражения (\ref{ConRf1}) соотвествует следующее условие для функций $\Phi_i$: $$\Phi_0=\Phi_1,~\Phi_{i}=\Phi_{-i},~~i=1,\ldots.$$ Для того, что бы получить теперь конечную цепочку необходимо поставить условие отражение с другого конца цепочки на некотром шаге $q$, полагая: $$\phi_{q-i}=-\phi_{q+1+i},~i=0,1,\ldots,q. \tag{2.40}\label{ConRf2}$$ При $i=q$ имеем соотношение $\phi_0=\phi_{2q+1}=0$. Не трудно видеть, что в этом случае уравнения с номерами $q+1+i$ переходят в уравнения с номерами $q-i$ для указанных значений индекса $i$. В результате получаем замкнутую конечную цепочку уравнений с номерами $i=1,\ldots,q$. В частности, при $q=3$ имеем систему уравнений следующего вида: $$\dot{\phi}_1 =M\Big(e^{\phi_2}-e^{\phi_1}+e^{-\phi_1}-1),$$ $$\dot{\phi}_2 = M\Big(e^{\phi_3}-e^{\phi_2}+e^{-\phi_2}-e^{-\phi_2}),$$ $$\dot{\phi}_3 =M\Big(2e^{-\phi_3}-e^{\phi_3}-e^{-\phi_2}).$$ Вновь, переходя к переменным $x,y,z$, запишем эту систему в полиномиальном виде: $$\dot{x}=M(y-x)x+M(1-x),$$ $$\dot{y}=M(z-y)y+M(1-y/x),$$ $$\dot{z}=M(2-z^2-z/y).$$ Условия отражения можно распространить и на другие типы цепочек, построенными на вспомогательных уравнениях одновременно и с правыми и левыми сдвигами.
7.2.10. Системы конечной длины общего вида
Результаты, полученные для цепочек конечной длины формально можно обощить, не прибегая к той или иной процедуре ограничения длины бесконечных цепочек. Рассмотрим систему (\ref{EqUM}) относительно вектора ${\bf U}=\{\Phi_0,\Phi_1,\ldots,\Phi_n\}$ с произвольной вещественной матрицей $\hat{{\bf M}}$. Введем следующее представление для функций $\Phi_i$, полагая: $$\Phi_i=Q_i(t)\Phi_0,~i=1,\ldots,n.\tag{2.41}\label{DefQPhi0}$$ Подставляя эти соотношения в систему (\ref{EqUM}), находим: $$\frac{1}{\Phi_0}\frac{d\Phi_0}{dt}=M_{00}+\sum\limits_{k=1}^nM_{0k}Q_k(t),$$ $$\frac{dQ_i}{dt}=-Q_i\frac{1}{\Phi_0}\frac{d\Phi_0}{d t}+M_{i0}+\sum\limits_{k=1}^nM_{ik}Q_k,~i=1,\ldots,n.$$ Исключая из последних уравнений $\Phi_0$ с помощью первого уравнения, приходим к нелинейной системе уравнений, относительно $n$ функций $Q_i$ следующкго вида: $$\frac{dQ_i}{dt}=M_{i0}-Q_iM_{00}+\sum\limits_{k=1}^n\Big(M_{ik}-Q_iM_{0k}\Big)Q_k,~i=1,\ldots,n.\tag{2.42}\label{EqQ}$$
В матричном виде эту систему можно записиать в следующей форме: $$\frac{d{\bf Q}}{dt}={\bf m}+\Big(\hat{{\bf M}}_1-M_{00}\Big){\bf Q}-({\bf n},{\bf Q}){\bf Q},\tag{2.43}\label{EqQM}$$ где ${\bf Q}=\{Q_1,\ldots,Q_n\}$, ${\bf m}=\{M_{10},\ldots,M_{n0}\}$, ${\bf n}=\{M_{01},\ldots,M_{0n}\}$, $({\bf n},{\bf Q})=\sum\limits_{k=1}^nn_kQ_k$ и матрица $\hat{{\bf M}}_1$ предсталяет собой часть матрицы $\hat{{\bf M}}$ без первой строки и первого столбца. Пусть теперь функции $Q_i$ являются дифференцируемыми функциями компонент другого вектора ${\bf x}=\{x_1,\ldots,x_n\}$. Будем полагать, что зависмость ${\bf Q}_i={\bf Q}_{i}({\bf x})$ такова, что матрица $\hat{{\bf J}}$ с компонентами: $$J_{km}=\frac{\partial Q_k}{\partial x_m},~k,m=1,\ldots,n,$$ является невырожденной. Тогда система (\ref{EqQM}) преобразуется к следующему виду: $$\frac{d{\bf x}}{dt}=\hat{{\bf J}}^{-1}({\bf x}){\bf m}+\Big(\hat{{\bf J}}^{-1}({\bf x})\hat{{\bf M}}_1\hat{{\bf J}}({\bf x})-M_{00}\Big){\bf x}-\Big({\bf n}\hat{{\bf J}}({\bf x}),{\bf x}\Big){\bf x}.\tag{2.44}\label{EqxM}$$
В качестве примера рассмотрим модель в размерности $n=2$, которая соответствует простейшему выбору функций $Q_1(t)=x+K_0,~Q_2(t)=y+L_0$. Уравнения этой модели при произвольной матрице $\hat{{\bf M}}$ размерности $3\times 3$ имеют в этом случае такой вид: $$\dot{x}=R_{10}x+R_{01}y+R_{20}x^2+R_{11}xy+R_{00},$$ $$\dot{y}=Q_{10}x+Q_{01}y+Q_{02}y^2+Q_{11}xy+Q_{00}, \tag{2.45}\label{EqM21}$$ где: $$R_{10}=M_{11}-M_{00}-L_0M_{02}-2K_0M_{01},$$ $$R_{01}=M_{12}-K_0M_{02},~~R_{20}=-M_{01},~~R_{11}=-M_{02},$$ $$R_{00}=M_{10}+L_0M_{12}+K_0(M_{11}-M_{00}-L_0M_{02}-K_0M_{01}),$$ $$Q_{01}=M_{22}-M_{00}-K_0M_{01}-2L_0M_{02},$$ $$Q_{10}=M_{21}-L_0M_{01},~~Q_{02}=-M_{02},~~Q_{11}=-M_{01},$$ $$Q_{00}=M_{20}+k_0M_{21}+L_0(M_{22}-M_{00}-K_0M_{01}-L_0M_{02}).$$ Количество независимых коэффициентов этой модели равно 10, а число независмых параметров равно 11, т.е. на 1 больше. Коэффиценты линейной части этой модели могут быть выбраны произвольно, а коэффиценты квадратичной части в каждом из уравнений модели определяются только двумя независимыми параметрами $M_{01}$ и $M_{02}$. Это указывает на некоторую выделенность интегрируемых с помощью рассматриваемых подстановок моделей среди всех типов модей с квадратичной нелинейностью.
7.2.11. Интегралы движения цепочек конечной длины
Для случая цепочек конечной длины вычисление интегралов движения производится по общим схемам, рассмотренным ранее для бесконечных цепочек. Поскольку динамические системы для цепочек конечной длины играют важную роль в прикладных задачах, здесь будут рассмрены некоторые примеры построения интегралов движения.
A. Циклические цепочки
Для циклических цепочек матрица $\hat{{\bf M}}$ размерности $q\times q$ представлет собой циклическую матрицу или циркулянт [Belman69] и может быть записана в следующем общем виде: $$\hat{{\bf M}}=\left(\begin{array}{ccccc} M_0 & M_1 & M_2 & \ldots & M_q\\ M_{q} & M_0 & M_1 & \ldots & M_{q-1}\\ \ldots & \ldots & \ldots \ldots & \ldots\\ M_{1} & M_2 & M_3 & \ldots & M_0\end{array}\right).\tag{2.46}\label{DefCM}$$ Собственные числа этой матрицы являются не кратными и имеют следующий вид: $$\lambda_k = p(r_k),~k=1,\ldots,q,$$ где $p(x)=M_0+M_1x+\dots+M_{q}x^{q-1}$ и $r_k=e^{2\pi/k}$. Правые собственные вектора циклической матрицы имеют следующий вид: $${\bf u}_k = {\rm column}\{1,r_k,r_k^2,\ldots,r_k^{q-1}\},~k=1,\ldots,q.$$ Матрица левых собственных векторов вычисляется как обратная к матрице правых собственных векторов с темиже собственными числами.
В частности, для случая $q=3$, соответствующему модели (\ref{Eqxy}), необходимо решать систему из трех уравнений следующего вида: $$\dot{\Phi}_0=M_0\Phi_0+M_1\Phi_1+M_2\Phi_2,$$ $$\dot{\Phi}_1=M_0\Phi_1+M_1\Phi_2+M_2\Phi_0,$$ $$\dot{\Phi}_2=M_0\Phi_2+M_1\Phi_0+M_2\Phi_1.\tag{2.47}\label{EqPhiM3}$$ Характеристическое уравнение для этой системы имеет такой вид: $$(M_0-\lambda)^3+M_1^3+M_2^3-3(M_0-\lambda)M_1M_2=0,$$ а соответствующие его корни такой: $$\lambda_1=M_0+M_1+M_2,~~\lambda_{2,3}=M_0-(M_1+M_2)/2\pm i(M_1-M_2)\sqrt{3}/2.$$ Правые собственные вектора циклической матрицы:
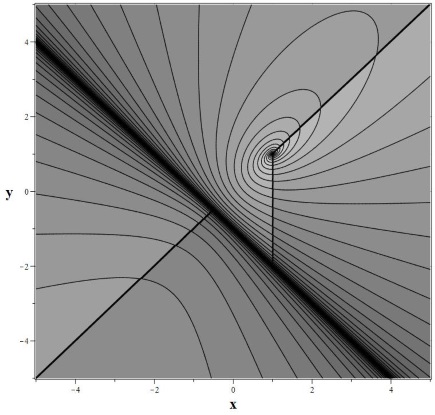
$$\hat{{\bf M}}=\left(\begin{array}{ccc} M_0 & M_1 & M_2\\ M_2 & M_0 & M_1\\ M_1 & M_2 & M_0 \end{array}\right),\tag{2.48}\label{DefCM3}$$ соотвествующей системе (\ref{EqPhiM3}) имеют такой вид: $${\bf v}_1=\left(\frac{M_1-M_2-i\sqrt{3}(M_1+M_2)}{M_1+M_2+i\sqrt{3}M_1},1,\frac{2M_1+M_2-i\sqrt{3}M_2}{M_1+M_2+i\sqrt{3}M_1}\right),$$ $${\bf v}_2=\left(-\frac{M_1-M_2+i\sqrt{3}(M_1+M_2)}{2M_1+2M_2+i\sqrt{3}M_2},-\frac{M_1+2M_2-i\sqrt{3}M_2}{2M_1+2M_2+i\sqrt{3}M_2},1\right),$$ $${\bf v}_3=(1,1,1).$$ Используя для модели (\ref{Eqxy}) схему вычисления интегралов движения для случая некратных собственных чисел, приходим к одному интегралу движения следующего вида: $$F(x,y)=\frac{(y+x+1)^2}{(y+x+1)^2-3(yx+x+y)},\quad H(x,y)=\frac{\sqrt{3}\gamma (y-1)}{2x-y-1}.$$ Фазовый портрет этой системы для $k_1=1,k_2=2,k_3=3$ представлен на рис. 7.2.1. Динамическая система (\ref{Eqxy}) имеет одну собую точку $x_0=1,y_0=1$ типа фокус. Кроме этого имеется особенность вдоль прямой $x+y+1=0$, на которой значение интеграла обращается в бесконечность. Три дополнительных отрезка прямых, проходящих через особую точку, указывают на положение точек, где арктангенс скачком изменяется на $\pi$. Эти особенности устранимы. Видно, что фазовые кривые на рис.7.2.1a переходят через линии скачков непрерывно.
 а а |
 b b |
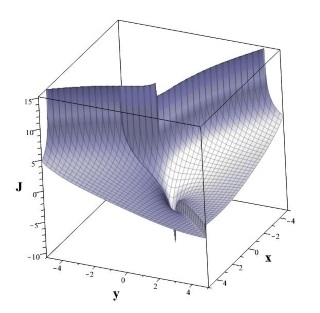
| Рис. 7.2.1. Фазовый портрет циклической цепочки (\ref{Eqxy}), a – фазовый портрет, b – функция интеграла: J=J(x,y) | |
Решения системы (\ref{EqPhiM3}) можно записать в векторной форме: $${\bf u} = P_1 {\bf u}_1 e^{\lambda_1 t}+P_2{\bf u}_2 e^{\lambda_2 t}+P_3{\bf u}_3 e^{\lambda_3 t},$$ где ${\bf u}={\rm column}\{\Phi_0,\Phi_1,\Phi_3\}$, $P_i$ - произвольные постоянные, а ${\bf u}_{k},~k=1,2,3$ - собственные вектора матрицы $\hat{{\bf M}}$ (\ref{DefCM3}). Если $\Phi_0,\Phi_1,\Phi_2$ - решения этой линейной системы уравнений. Тогда решения уравнений (\ref{EqCL3}) и (\ref{Eqxy}) имеют такой вид: $$\phi_0=\ln\left(\frac{\Phi_1}{\Phi_0}\right),~~\phi_1=\ln\left(\frac{\Phi_2}{\Phi_1}\right),~~x= \frac{\Phi_1}{\Phi_0},~~y=\frac{\Phi_2}{\Phi_1}.\tag{2.49}\label{Solxy}$$ В общем случае решения уравнений (\ref{EqCLat}) сводятся к решению линейной системы уравнений (\ref{EqPhin}) с циклической матрицей (\ref{DefCM}). В результате общее решение вспомгательных уравнений можно записать в следующем виде: $${\bf u}=\sum\limits_{k=1}^q P_k{\bf u}_k e^{\lambda_k t}.$$ Соотвественно, решения нелинейной циклической цепочки будут иметь такой вид: $$\phi_k=\ln\left(\frac{\Phi_{k+1}}{\Phi_k}\right),~~k=0,\ldots,q-2.\tag{2.50}\label{Solphik}$$
B. Ограниченные цепочки
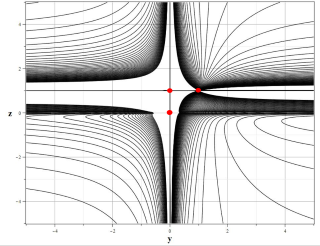
В случае ограниченных цепочек типа (\ref{Eqxyz}) вспомогательные уравнения имеют вид системы уравнений (\ref{EqUM}), в которой ${\bf U}={\rm column}\{\Phi_0,\Phi_1,…,\Phi_q\}$, а матрица $\hat{{\bf M}}$ имеет размерность $(q+1)×(q+1)$ и такой вид: $$\hat{{\bf M}}=\left(\begin{array}{cccccccc} M_0 & M_1 & M_2 &\ldots &M_n & 0&\ldots &0 \\ 0 & M_0 & M_1 &\ldots & M_{n-1}& M_n &\ldots & 0\\ \ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\ 0 & 0 & 0 &\ldots & M_0 & M_1 &\ldots &M_n\\ 0 & 0 & 0 &\ldots & 0 & M_0 &\ldots & M_{n-1}+M_n\\ \ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\ 0 & 0 & 0 &\ldots & 0 & 0 & \ldots & M_0+\cdots+M_n \end{array}\right).$$ Без ограничения общности мы полагаем $p=0$. Данная матрица имеет два различных собственных числа: $\lambda_1=M_0+\cdots+M_n,\lambda_2=\lambda_3=\cdots=\lambda_q=M_0$, одно из которых $q$ раз вырождено. Это означает, что для вычисления интегралов следует использовать соотношения (\ref{DefJLL}). Для случая $q=3$ интегралы движения имеют следующий вид: $$J_{yz}=M_1 \tau(z)+\frac{zy-1}{y(z-1)},$$ $$J_{xyz}=(M_1^2)/2 \tau^2 (z)-\Big(M_1\frac{1-yz)}{y(1-z)}+M_2\Big) \tau(z)+\frac{1-xyz}{xy(1-z)},$$ где $$\tau(z)=1/(M_1+M_2 ) \ln\left|\frac{z}{z-1}.\right|$$ На рис. 7.2.2 представлен фазовый портрет системы (\ref{Eqxyz}) вместе с графиком интеграла $J_{yz}$. Система имеет четыре особых точки с координатами: $P_1=(0,0,0),~P_2=(0,0,1),~P_2=(0,1,1),~P_4=(1,1,1)$.
 a a |
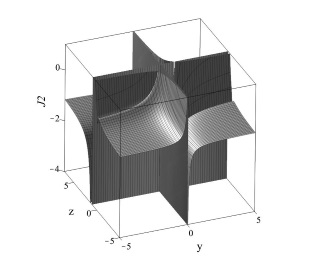 b b |
|
|
||
С. Линеаризуемые конечномерные модели общего вида
Интегралы движения для моделей конечной размерности вычисляются по общей схеме, изложенной в разделе 7.2.6. Для модели (\ref{EqxM}) , имеющей размерность $n=2$, существует один интеграл движения, который в случае, когда все три собственных числа $\lambda_0,\lambda_1,\lambda_2$ матрицы $\hat{{\bf M}}$ различны, имеет такой вид: $$J_{12}=(\ln|Q_1/Q_0|)/(\lambda_0-\lambda_1 ) -\ln|Q_2/Q_0|/(\lambda_0-\lambda_2)$$, где $${\bf Q}_k=v_k^0+v_k^1 x+v_k^2 y,k=0,1,2$$, а ${\bf v}_k$ - левые собственные вектора матри $\hat{{\bf M}}$ размерности $3$ общего вида. Поскольку частным случаем матрицы $\hat{{\bf M}}$ являются варианты циклической и ограниченной матриц, рассмотренные выше, то интерес представляет только случай симметричной матрицы. Поскольку для симметричной матрицы собственные числа и собственные вектора вещественные, и, кроме того, собственные вектора ортогональны, то удобно вместо самой матрицы задавать сами собственные числа и собственные вектора. Выберем в качестве собственных векторов матрицы $\hat{{\bf M}}$ следующие три вектор: $${\bf v}_1=\sqrt{2}/2 (\cos(\theta),\sin(\theta),1),$$ $${\bf v}_2=\sqrt{2}/2(-\cos(\theta), -\sin(\theta),1),$$ $${\bf v}_3=(-\sin(\theta),\sin(\theta),0),$$ а в качестве собственных чисел, им соответствующих, три вещественных числа $\lambda_0,\lambda_1,\lambda_2$. В этом случае интеграл движения примет следующий вид: $$J_{12}=\frac{1}{(\lambda_0-\lambda_1)} \ln\left|\frac{(cos(\theta)+\sin(\theta)x+y)}{(x \cos(\theta)-\sin(\theta) )}\right|-\frac{1}{\lambda_0-\lambda_2}\ln\left|\frac{-\cos(\theta)-\sin(\theta)x+y}{x cos(\theta)-\sin(\theta)}\right|.$$ Для случая $\theta=\pi/3$ и $\lambda_0=1,\lambda_1=2,\lambda_2=3$ матрица $\hat{{\bf M}}$ будет иметь такой вид: $$\hat{{\bf M}}=1/8 \left(\begin{array}{ccc}((21 &-3\sqrt{3} &-2\\-3\sqrt{3} & 15 & -2\sqrt{3}\\-2 &-2\sqrt{3} & 12\end{array}\right)$$, а сама динамическая система – такой: $$\dot{x}=1/8 \Big(6x+2\sqrt{3}y-3\sqrt{3} x^2+2xy+3\sqrt{3}\Big),$$ $$\dot{y}=1/8 \Big(2\sqrt{3} x+9y-2y^2-3\sqrt{3} xy+2\Big).\tag{2.51}\label{EqGLSysxy}$$ Фазовый портрет данной системы приведен на рис. (7.2.3). Три особые точки системы лежат на песечении трех особых прямых интеграла $J_{12}(x,y)$, соответствующих трем собственным векторам матрицы $\hat{{\bf M}}$. Одна из точек – седловая, а две другие – узлы. Один из узлов устойчивый, другой - неустойчивый.
 a a |
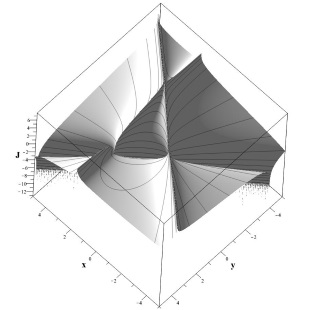 b b |
| Рис. 7.2.3. Фазовый портрет системы (\ref{EqGLSysxy}), $a$ – фазовый портрет, $b$- функция интеграла $J_{12}=J_{12}(x,y)$ | |
- Войдите на сайт для отправки комментариев
- 4035 просмотров