Отчет второго этапа

2. Качественный анализ космологических решений в обобщенной тензорно-скалярной теории гравитации с потенциалом Хиггса

(по статье С.В. Червон, В.М. Журавлев, К.А. Большакова)

2.1 Введение

       Подтверждение существования бозона Хиггса в 2012 году в экспериментах на Большом адронном коллайдере (БАК) явилось важным подспорьем для физиков-теоретиков. Около 25 лет прошло с тех пор как было предложено использовать стандартную модель хиггсовского бозона в космологии при рассмотрении космологической инфляции ранней Вселенной [1]. Экспериментальное открытие бозона Хиггса и уточнение его характеристик, включая массу бозона, подтвердили корректность и адекватность теории хиггсовского Бозона Ф. Безрукова и М. Шапошникова.

    В настоящей работе мы возвращаемся к первоисточнику теории инфлантона как хиггсовского бозона [1] с целью внесения уточнений на основе современных достижений теории космологической инфляции.

2.2 Фоновые уравнения хиггсовской инфляции

       В работе [1] рассматривается модель гравитации с неминимальным взаимодействием со скалярным полем Хиггса $$S_J=\int d^4x \sqrt{-g}\left\{\frac{M_P^2}{2}F(\phi)R+\omega(\phi)X-V(\phi)\right\}\tag{2.1}\label{act-J}$$ Здесь, в отличии от работы [1], используется сигнатура $(-+++)$ чтобы адаптировать действие к таковому,
представленному в работе [2]. В исходном действии (\ref{act-J}) поле $\phi$ отождествляется с полем Хиггса $h$. Значение функции неминимального взаимодействия $F(\phi)$, кинетической функции $\omega$, кинетической энергии $X$ и потенциала $V(\phi)$ таковы: $$F(\phi)=\frac{M^2+\xi \phi^2}{M_P^2},~~\omega =1,~~X=-\frac{1}{2}\phi_{,\mu} \phi_{,\nu} g^{\mu\nu},~~V(\phi)=\frac{\lambda}{4}\left(\phi^2-v^2\right)^2.\tag{2.2}\label{FwV}$$
Отметим, что в действии (\ref{act-J}) метрика $g_{\mu\nu}$ записана в картине Йордана.

      Утверждается, что при больших, но ограниченных значениях коэффициента $\xi$: $1\ll \sqrt{\xi}\ll 10^{17}$ $M \simeq M_P$ с высокой точностью.

      Аналогичная модель была рассмотрена ранее в работе [4]. В частности там рассматривается неминимальнаягравитация с потенциалом Гинзбурга-Ландау с действием следующего вида $$\label{act-GL}S_J=\int d^4x \sqrt{-g}\left\{\frac{1+\varkappa^2\xi \phi^2}{2\varkappa^2} R-\frac{1}{2}\phi_{,\mu} \phi_{,\nu} g^{\mu\nu}-\frac{\lambda}{4}\left(\phi^2-v^2\right)^2\right\}.\tag{2.3}$$

      Полагая, что в конце инфляции $\phi \simeq v$, а не $\simeq 0$, настоящее значение планковской массы определяется соотношением $$M^2_P=\frac{1+\varkappa^2\xi v}{\varkappa^2},~~\varkappa^2 \neq M_P^{-2}= \varkappa^2_N.$$

      Вводя новую переменную $\delta^2=\varkappa^2\xi v$ для отношения $$\frac{\varkappa^2}{\varkappa^2_N}=\frac{M_P^2}{M^2}=1+\delta^2,$$ отмечается, что спектральный индекс для такой модели является функцией двух свободных параметров $\xi$ и $\delta^2$, причем $\xi \geq 0$. Причем факт близости $\xi$ к $0$ позволяет нам рассматривать $\xi \ll 1$, что не допускается в модели Безрукова-Шапошникова [1].

      Запишем уравнения космологической динамики для действия (\ref{act-J}) на основе (5)-(7) работы [2].

$$\label{E1} 3(M^2+\xi\phi^2)H^2+3H(2\xi\phi\dot{\phi})-\frac{1}{2}\dot{\phi}^2- \frac{\lambda}{4}\left(\phi^2-v^2\right)^2=0,\tag{2.5}$$ $$\label{E2} 3(M^2+\xi\phi^2)H^2+2H(2\xi\phi\dot{\phi})+2(M^2+\xi\phi^2)\dot{H}+2\xi (\dot{\phi}^2+\phi\ddot{\phi})+\frac{1}{2}\dot{\phi}^2 -V(\phi)=0,\tag{2.6}$$ $$\label{E3}\ddot{\phi}+3H\dot{\phi}+\lambda\phi (\phi^2-v^2)-6H^2 2\xi\phi -3\dot{H}2\xi\phi=0.\tag{2.7}$$

     Отметим значение и размерность параметров, входящих в действие. $$M_P=2.4 10^{18} GeV, ~~1\ll\sqrt{\xi}\ll 10^{17}, ~~\lambda \simeq 10^{-13},~~v=246 GeV,~~m_H=125 GeV.$$

     Уравнения \eqref{E1}-\eqref{E3} перепишем для любого потенциала $$\label{E1-V} 3(M^2+\xi\phi^2)H^2+3H(2\xi\phi\dot{\phi})-\frac{1}{2}\dot{\phi}^2- V(\phi)=0,\tag{2.8} $$

$$\label{E2-V}
3(M^2+\xi\phi^2)H^2+2H(2\xi\phi\dot{\phi})+2(M^2+\xi\phi^2)\dot{H}+2\xi (\dot{\phi}^2+\phi\ddot{\phi})+\frac{1}{2}\dot{\phi}^2 -V(\phi)=0,\tag{2.9}$$

$$\label{E3-V} \ddot{\phi}+3H\dot{\phi}+V' - 6H^2 2\xi\phi -3\dot{H}2\xi\phi=0.\tag{2.10}$$

     Введем в рассмотрение суперпотенциал в форме Журавлева-Червона [4,5] $$\label{W-ZC} W(\phi)=\frac{1}{2}\dot{\phi}^2+V(\phi),~~ W'=\ddot{\phi}+V'.\tag{2.11}$$

Для упрощения записи уравнений поля введем новое поле $\Psi$ следующим образом
$$\label{psi} \Psi=M^2+\xi \phi^2,~~\dot{\Psi}=2\xi\phi\dot{\phi}.\tag{2.12}$$

Система уравнений \eqref{E1-V}-\eqref{E3-V} принимает следующий вид: $$\label{E1-W} 3\Psi H^2+3H\dot{\Psi}-W(\Psi)=0,\tag{2.13} $$

$$\label{E2-W} \ddot{\Psi}+ \frac{\dot{\Psi}^2}{4\xi (\Psi-M^2)}-H\dot{\Psi} +2\Psi\dot{H}=0,\tag{2.14}$$

$$\label{E3-W}3H\frac{\dot{\Psi}^2}{4\xi (\Psi-M^2)}+\dot{W}-3\dot{\Psi}(2H^2+\dot{H})=0.\tag{2.15}$$

Исследуем приближения, рассмотренные в статье [1].

2.3 Слабое поле Хиггса в J-картине

     Для малых значений хиггсовского поля имеем: $$h\equiv \phi \simeq \chi, ~~\Omega^2\simeq 1 \Rightarrow \xi\phi^2\simeq 0,~~\xi\gg 1 \Rightarrow \phi^2 \simeq 0.$$ Здесь $\chi$ приведенное к каноническому виду поле в картине Эйнштейна.

     В приближении малых значений хиггсовского поля уравнения космологической динамики принимают вид: $$\label{E1-w} 3(M^2)H^2+3H(2\xi\phi\dot{\phi})-\frac{1}{2}\dot{\phi}^2-\frac{\lambda}{4}v^4=0,\tag{2.16}$$

$$\label{E2-w} 3(M^2)H^2+2H(2\xi\phi\dot{\phi})+2(M^2)\dot{H}+2\xi (\dot{\phi}^2+\phi\ddot{\phi})+\frac{1}{2}\dot{\phi}^2 -\frac{\lambda}{4}v^4=0,\tag{2.17}$$

$$\label{E3-w}\ddot{\phi}+3H\dot{\phi}-\lambda v^2\phi -6H^2 2\xi\phi -3\dot{H}2\xi\phi=0.\tag{2.18}$$

     В режиме медленного скатывания имеем решение $$\label{sr-w} \phi=\phi_*=const.,~~H=H_*=const.,~~3M^2H_*^2=\frac{\lambda}{4}v^4, ~~\xi=-M^2/v^2.\tag{2.19}$$ Ясно, что это решение не является физически обосновано, так как $\xi \gg 1>0$.

2.3.1 Режим медленного скатывания для поля Хиггса в J-картине

     Учитывая $\dot{\phi}^2 \simeq 0,~~\phi\ddot{\phi} \simeq 0$ запишем систему уравнений космологической динамики $$\label{E1-sr}
3(M^2+\xi\phi^2)H^2+3H(2\xi\phi\dot{\phi})- \frac{\lambda}{4}\left(\phi^2-v^2\right)^2=0,\tag{2.20}
$$

$$\label{E2-sr}
3(M^2+\xi\phi^2)H^2+2H(2\xi\phi\dot{\phi})+2(M^2+\xi\phi^2)\dot{H}-V(\phi)=0,\tag{2.21}
$$

$$\label{E3-sr}
3H\dot{\phi}+\lambda\phi (\phi^2-v^2)-6H^2 2\xi\phi -3\dot{H}2\xi\phi=0.\tag{2.22}
$$

     Далее, вычитая \eqref{E2-sr} из \eqref{E1-sr} и интегрируя полученное уравнение, находим решение (анзац)
$$\label{H-fi}
H=H_0 \sqrt{M^2+\xi \phi^2},~~\dot{H}=H_0\frac{\xi \phi \dot{\phi}}{\sqrt{M^2+\xi \phi^2}}.\tag{2.23}
$$

     Подставляем анзац \eqref{H-fi} в уравнение \eqref{E1-sr}, находим решение
$$\label{sr-sol} t-t_*=\frac{6\xi}{\sqrt{3\lambda}b}\left[\tanh^{-1} \frac{(b^{-1}\sqrt{K+1}\Psi)}{\sqrt{K+1}}- \tanh^{-1}\frac{(b^{-1}\sqrt{K-1}\Psi)}{\sqrt{K-1}}\right].\tag{2.24}
$$ Здесь $$\label{sr-sol-2} \Psi^2=M^2+\xi \phi^2,~~ K=\frac{2\sqrt{3}}{\sqrt{\lambda}}H_0\xi,~~b^2=M^2+\xi v^2.\tag{2.25}$$

     В нашем подходе мы не рассматриваем уравнение поля \eqref{E3}, которое может быть получено как следствие уравнений \eqref{E1}-\eqref{E2}. В приближении медленного скатывания это свойство не выполняется.

    Найдем число е-фолдов, используя определение $N$: $$\label{N-sr} N= \int H dt= \int \frac{H d\phi}{(d\phi/dt)}=\int \frac{H d\phi}{\dot{\phi}}=\int \frac{H d\Psi}{\dot{\Psi}}=H_0\int \frac{\Psi d\Psi}{\dot{\Psi}}.\tag{2.26}$$

    Из \eqref{E1-sr} выразим $\dot{\phi}$ и подставим, вместе с анзацем \eqref{H-fi}, в формулу \eqref{N-sr}. Выполняя интегрирование получаем $$\label{N-sr-f} N=\frac{\sqrt{3}H_0}{2}\left\{\frac{\ln \left[(B_-)\Psi^2 -A\right]}{B_-} - \frac{\ln \left[(B_+)\Psi^2 -A\right]}{B_+}\right\},\tag{2.27}$$ где $$\label{AB} A=\frac{\sqrt{\lambda}}{2\xi}b^2,~~B_{\pm}=\frac{\sqrt{\lambda}}{2\xi} \pm H_0\sqrt{3}.\tag{2.28}$$

     Повторный расчет по MAPLE дает $$N=-\frac{6\xi H_0}{\sqrt{6\lambda}}\left[\frac{\ln \left( -b^2+(c+1)\Psi^2\right)}{c+1}+\frac{\ln \left( b^2+(c-1)\Psi^2\right)}{c-1}\right] $$
где $$c^2=\frac{12\xi^2H_0^2}{\lambda}$$
Другая возможность -- подставить анзац \eqref{H-fi} в уравнение поля \eqref{E3-sr}.

2.3.2 Поле Хиггса в E-картине

      Конформное преобразование  $$\label{Omega}\hat{g}_{\mu\nu}=\Omega^2 g_{\mu\nu},~~\Omega^2=1+\frac{\xi\phi^2}{M_P^2}\tag{2.29}$$  с учетом преобразования хиггсовского поля
 $$\label{h-chi}  \frac{d\chi}{d\phi}=\Omega^{-2}\sqrt{\Omega^2+6\xi^2\phi^2/M_P^2}\tag{2.30} $$  приводит к действию в картине Эйнштейна  $$\label{act-E} S_E=\int d^4x \sqrt{-\hat{g}}\left\{\frac{M_P^2}{2}\hat{R}+\omega(\phi)\hat{X}-V_E(\phi)\right\}.\tag{2.31}$$

     Здесь $\omega =1$ когда $\hat{X}=-\frac{1}{2}\chi_{,\mu} \chi_{,\nu} \hat{g}^{\mu\nu}$. При этом потенциал имеет вид $$ V_E=\frac{1}{\Omega^4}V(\phi)= \frac{1}{\Omega^4}\frac{\lambda}{4}\left(\phi^2-v^2\right)^2.$$

     В терминах поля $\phi$, когда $\hat{X}=-\frac{1}{2}\phi_{,\mu} \phi_{,\nu} \hat{g}^{\mu\nu}$ кинетическая функция $\omega$ такова: $$\omega (\phi)=M_P^2 \left[\frac{6\xi^2\phi^2+\xi \phi^2+M_P^2}{\left(M_P^2+\xi\phi^2\right)^2}\right].$$

     Для записи уравнений космологической динамики потребуется производная от кинетической функции $\omega$ по полю $\phi$. Прямое вычисление дает: $$\omega_{,\phi}=\frac{2\xi\phi}{M_P^2 \Omega^4}\left[1+6\xi -2\Omega^2\left(\Omega^2+6\xi^2\phi^2/M_P^2\right)\right].$$

     Уравнения ($E_1$) и ($E_2$) принимают вид: $$\label{E1-e-fr} 3M_P^2 H^2-\omega(\phi)X(\phi)-V_E(\phi)=0,\tag{2.32}$$

$$\label{E2-e-fr} 3M_P^2 H^2 +2M_P^2\dot{H}+\omega(\phi)X(\phi)-V_E(\phi)=0.\tag{2.33}$$

     При этом разность ($E_2$)-($E_1$) дает $$\label{E2-1-efr} M_P^2\dot{H}=-\omega X(\phi).\tag{2.34}$$

     Сумма этих уравнений приводит (стандартно) к выражению для потенциала $$\label{E2+1-efr} V_E(\phi)= M_P^2(3H^2+\dot{H}).\tag{2.35}$$

      Распишем подробно \eqref{E1-e-fr} $$\label{E1-efr-d} 3 H^2= \frac{\Phi \frac{1}{2}U(\phi)+M_P^2 \frac{\lambda}{4}(\phi^2-v^2)^2}{(M_P^2+\xi \phi^2)^2},\tag{2.36}$$ где $$\label{Phi-1} \Phi= \phi^2(6\xi^2+\xi)+M_P^2,~~U(\phi)=\dot{\phi}^2.\tag{2.37}$$ Также распишем подробно \eqref{E2-1-efr} $$\label{E2-1-efr-d} M_P^2\dot{H}=\frac{\Phi}{(M_P^2+\xi \phi^2)^2}\frac{1}{2}U(\phi).\tag{2.38}$$

2.3.3 Приведение к полному квадрату числителя \eqref{E1-efr-d}}

     Приведение к полному квадрату числителя в уравнении \eqref{E1-efr-d} позволяет найти $H$, вычислить $\dot{H}$ и подставить полученное выражение в \eqref{E2-1-efr-d} для дальнейшего анализа.

     Представим $U(\phi)$ в виде $$\dot{\phi}^2=U(\phi)=U_1(\phi)+U_2(\phi),$$ где $$U_2(\phi)= M_P \sqrt{2\lambda \frac{U_1(\phi)}{\Phi}}.$$

     Тогда, извлекая корень из \eqref{E1-efr-d}, получаем $$\label{E1-efr-sr} H= \frac{\sqrt{\Phi\frac{1}{2}U_1(\phi)}+ \frac{M_P\sqrt{\lambda}}{2}(\phi^2-v^2)}{\sqrt{3}(M_P^2+\xi \phi^2)}.\tag{2.39}$$

     Уравнение \eqref{E2-1-efr-d} позволяет получить ограничение на функцию $U_1(\phi)$:
$$\frac{dU_1}{d\Theta}+\frac{1}{\sqrt{2}}\frac{U_1}{\Phi}+M_P \sqrt{\lambda} \sqrt{\frac{U_1}{\Theta}}-\frac{2\xi}{M_P^2+\xi \Theta}\left[ \frac{1}{\sqrt{2}}U_1+\sqrt{\frac{U_1}{\Theta}}\frac{M_P}{2} \sqrt{\lambda}(\Theta-v^2)\right]=$$ $$\frac{\sqrt{3\Phi U_1}}{2M_P^2\phi (M_P^2+\xi\Theta)}\sqrt{U_1+M_P \sqrt{2\lambda \frac{U_1}{\Phi}}},~~\Theta=\phi^2.$$
Таким образом получена зависимость параметра Хаббла от скалярного поля. Отметим, что пространство решений уравнения (45) не пустое. Постоянное скалярное поле или $U_1=0$ удовлетворяет уравнению (45). При этом параметр Хаббла также есть величина постоянная и инфляционная стадия реализуется.

2.3.4 Слабое поле Хиггса в E-картине

    Для слабого поля Хиггса, как отмечается в работе \cite{BezSha2007}, $ h\equiv \phi \simeq \chi, ~~\Omega^2\simeq 1.$ В этом случае действие \eqref{act-J} и \eqref{act-E} совпадают и можно найти точное решение с использованием генерирующий функции для полиномиальных потенциалов [3].

   Как показано в монографии [3], выбор генерирующей функции $F_{gen}$, зависящей от скалярного поля $\phi$ произвольным образом, позволяет определить параметр Хиггса $H(\phi)$ и потенциал $V(\phi)$ следующим образом $$H(\phi)=\frac{M_P}{\sqrt{3}}F_{gen},~~V(\phi)= 3M_P^2H^2-2M_P^4\left(\frac{dH}{d\phi}\right)^2=-\frac{2M_P^2}{3}\left(\frac{dF_{gen}}{d\phi}\right)^2+\left(F_{gen}(\phi)+F_{gen}^*\right)^2,$$ где $F_{gen}^*$ некоторая постоянная.

   Далее для простоты записи полагаем $M_P^2=1$. Генерирующая функция вида $$F_{gen}=\lambda_0+\lambda_2 \phi^2,~~\lambda_0=\frac{\lambda_2}{3},~~\lambda_2=\frac{\sqrt{\lambda}}{2}$$ приводит к точному решению при ограничении на вакуумное среднее хиггсовского поля $v$: $v=\frac{M_P}{\sqrt{3}}$.

    Решение имеет следующий вид: $$\phi(t)=\phi_0 \exp \left(-2\sqrt{\frac{\lambda}{3}}t\right),$$

$$H(t)=\frac{1}{2}\sqrt{\frac{\lambda}{3}}\phi_0\exp \left(-4\sqrt{\frac{\lambda}{3}}t\right)+\frac{1}{6}\sqrt{\frac{\lambda}{3}},$$

$$a(t)=a_0\exp \left[\frac{1}{6}\sqrt{\frac{\lambda}{3}}t + \frac{\phi_0^2}{8}\left( 1-e^{4\sqrt{\frac{\lambda}{3}}t} \right)\right].$$

2.4. Качественный анализ системы уравнений

    Для выяснения асимптотических свойств исследуемой системы приведем ее к безразмерному виду, вводя следующие безразмерные переменные: $$\psi(\tau) = \frac{1}{M}\phi(t),~~z(\tau)= \frac{1}{MH_0}\frac{d\phi}{dt},~~h(\tau) = \frac{1}{H_0}H(t),~~\tau = H_0 t,~~\Lambda=\lambda\frac{M^2}{H_0^2},~~w=\frac{v}{M}.$$ Здесь $H_0$ - масштабный множитель для параметра Хаббла.

   Для анализа систему удобно привести к стандартной форме динамической системы. Соответствующие уравнения модели приводятся такому виду: $$\label{E20} \frac{d h}{d\tau} = \frac{1}{R(\psi,\xi)}\left(\xi\psi\ F(\psi,z,h)-G(\psi,z,h)\right);\tag{2.40}$$

$$\label{E30} \frac{d z }{d\tau} = -\frac{1}{R(\psi,\xi)}\Big( (1+\xi\psi^2)F(\psi,z,h)+6\xi\psi G(\psi,z,h)\Big);\tag{2.41}$$

$$\label{E40} \frac{d\psi}{d\tau}=z(\tau).\tag{2.42}$$

$$\label{E10}(1+\xi\psi^2)h^2-\frac{1}{3}\left(\frac{1}{2} z^2-6\xi h\psi z-\frac{\Lambda}{4}(\psi^2-w^2)^2\right)=0.\tag{2.43}$$

    В этих уравнениях введены обозначения: $$\label{DefF}F(\psi,z,h)=3h z+\Lambda(\psi^2-w^2)\psi-12h^2\xi\psi,\tag{2.44}$$

$$\label{DefG} G(\psi,z,h)=\frac{3}{2}h^2(1+\xi\psi^2) + 2\xi h\psi z+\Big(\xi+\frac{1}{4}\Big)z^2-\frac{\Lambda}{8}(\psi^2-w^2)^2,\tag{2.45}$$

$$\label{DefR}R(\psi,\xi)=1 + \xi(1+6\xi)\psi^2.\tag{2.46}$$

     Как видно, данная система не содержит явно параметры $M$ и $H_0$. Отсюда следует, что существенными параметрами являются только $\xi$ и $w$. Параметр $H_0$ может быть вычислен из требования  $\Lambda=1$ без ограничения общности, именно: $H_0 =\sqrt{\lambda M^2}$.
     В уравнениях этот параметр задает масштаб параметра Хаббла и одновременно масштаб времени в силу соотношения: $\tau = H_0 t$. Таким образом, полагая $\Lambda=1$ мы просто определяем временной масштаб в решениях.

     Положение особых точек динамической системы \eqref{E20}-\eqref{E10} определяется двумя алгебраическими уравнениями: $$ F(\psi_0,0,z_0)=(\Lambda(\psi_0^2-w^2)-12h_0^2\xi)\psi_0=0,$$ $$ G(\psi_0,0,z_0)=\frac{3}{2}h_0^2(1+\xi\psi_0^2)-\frac{\Lambda}{8}(\psi_0^2-w^2)^2=0.$$ Как показывает анализ этих уравнений система (\ref{E20})-(\ref{E10}) имеет при всех значениях $\xi>0$ только три особые точки на плоскости $(\psi,h)$:
$$ \begin{array}{lll}
1 & \psi_0=0,  & h_0 = \pm w^2\sqrt{\frac{\Lambda}{12}};\\
2 & \psi_0=-w, & h_0 = 0;\\
3 &\psi_0=w, & h_0 = 0;
\end{array}
$$
     Следует отметить, что структура модели такова, что решение $\psi_0\not=0$ и $h_0\not=0$ отсутствует, хотя небольшое изменение ее параметров могло бы привести к появлению пары особых точек и усложнению динамики системы.

    Точка $P_1$, соответствующая локальному максимуму потенциала. Точки $P_2-P_3$, соответствующие локальным минимумам являются притягивающими фокусами.

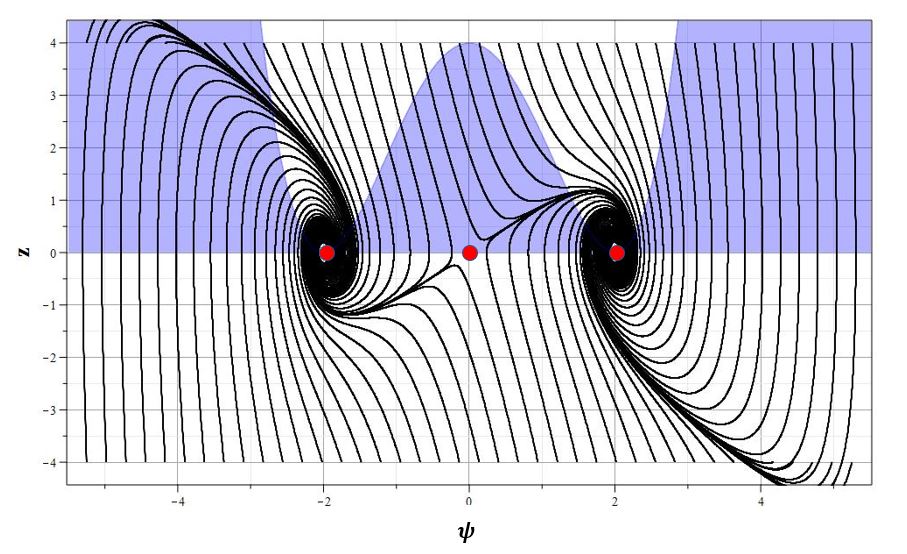
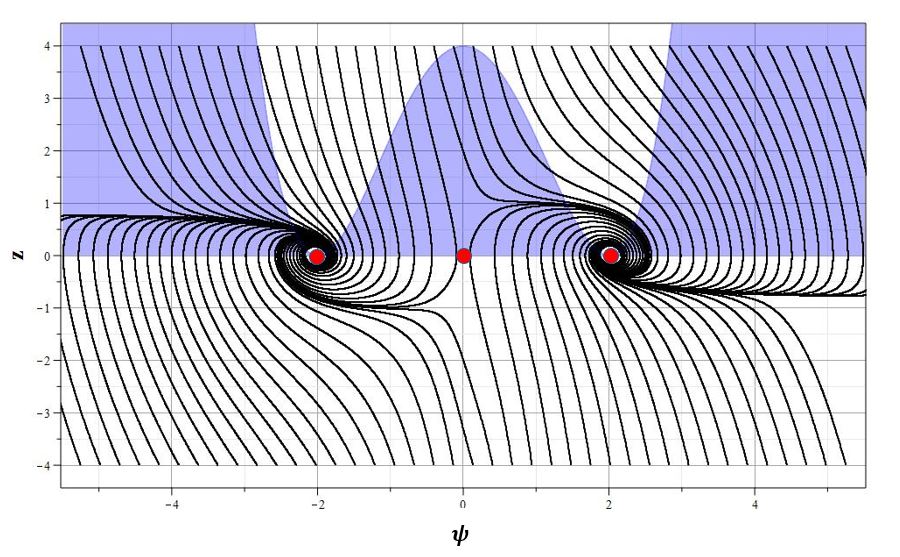
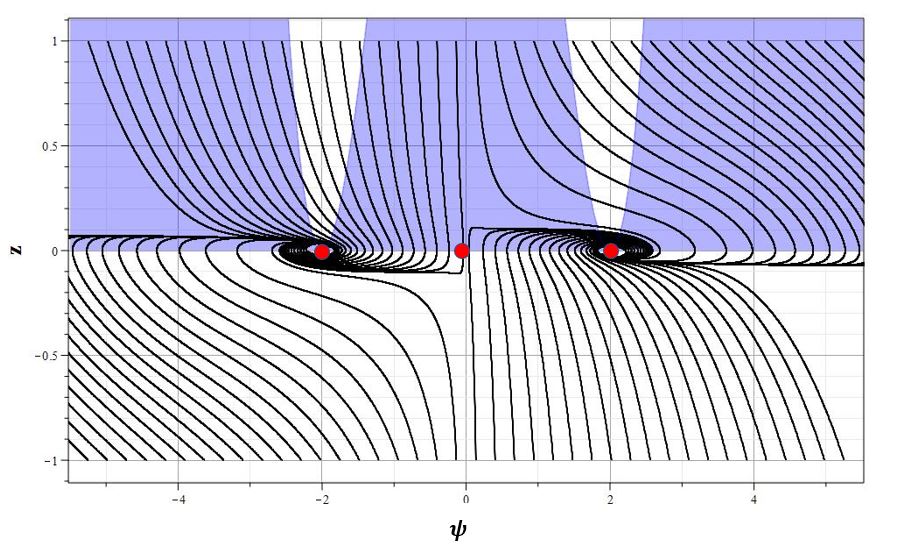
На рис. \ref{pic001}, \ref{pic1} и \ref{pic100} представлен фазовый портрет системы вблизи точек $P_1,P_2,P_3$ для значений  $w=2$ и трех значений $\xi=0.01,~\xi=1.0$ и $\xi=100.0$. Положение особых точек показано красными точками.

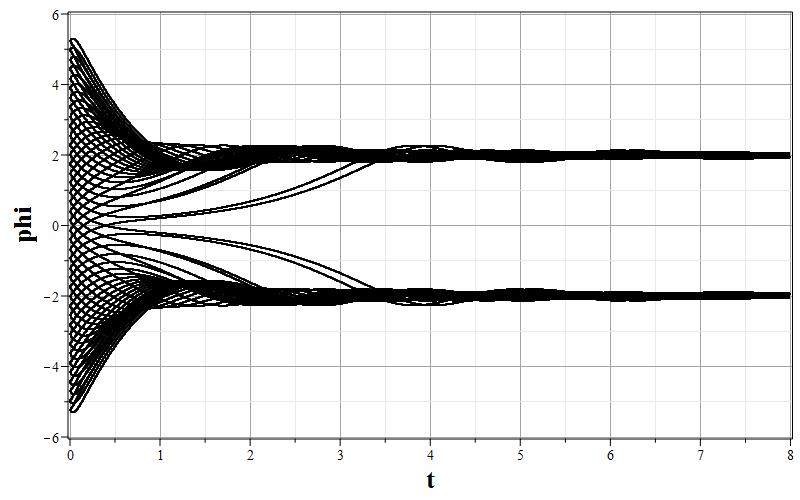
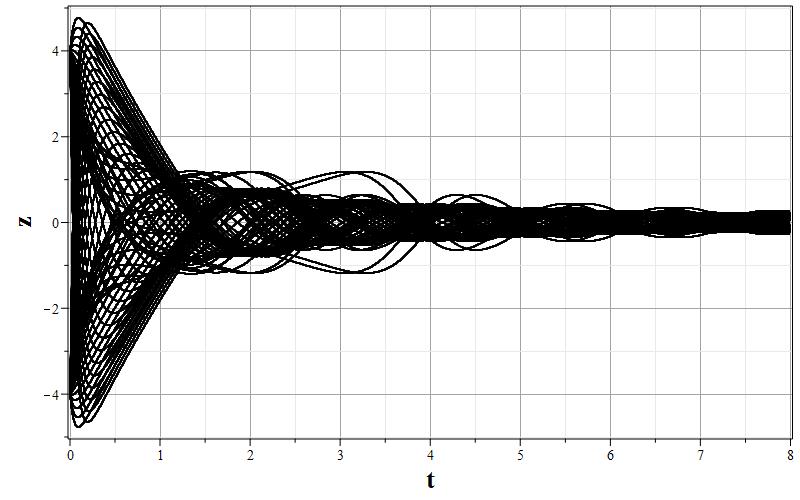
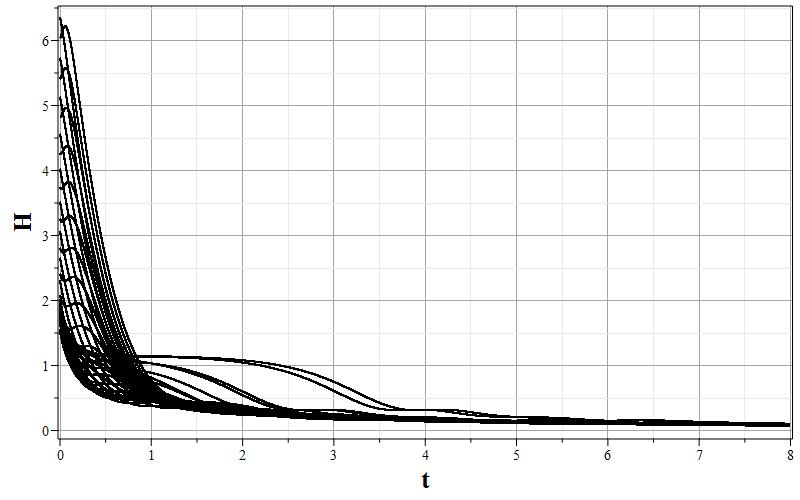
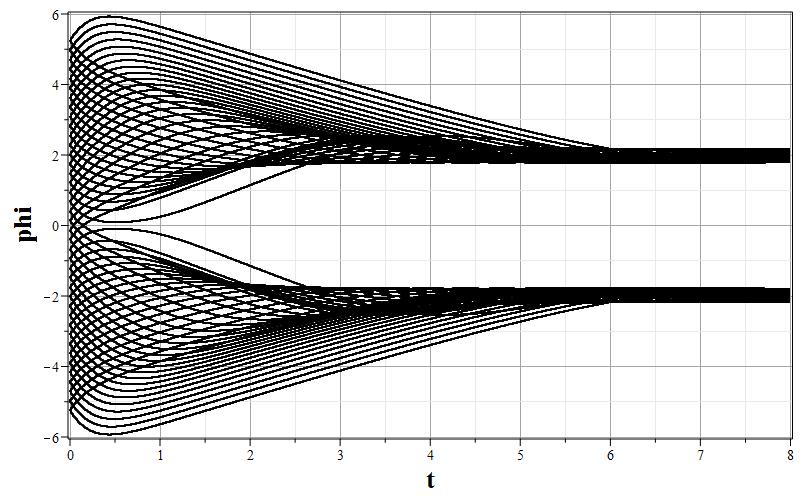
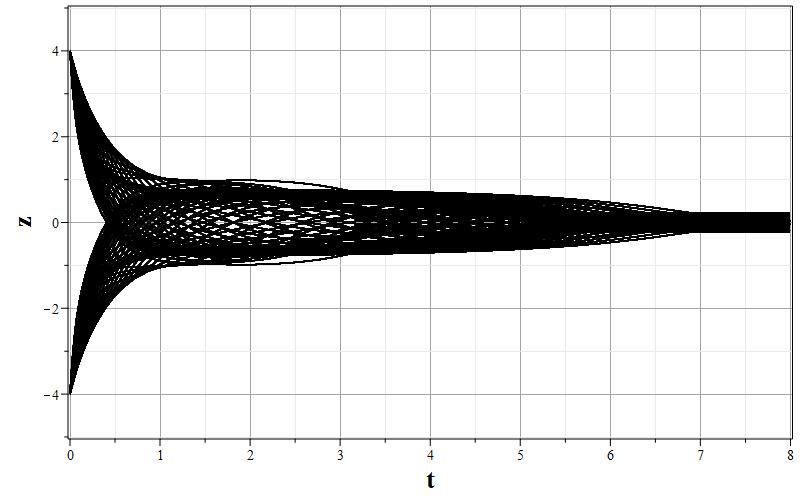
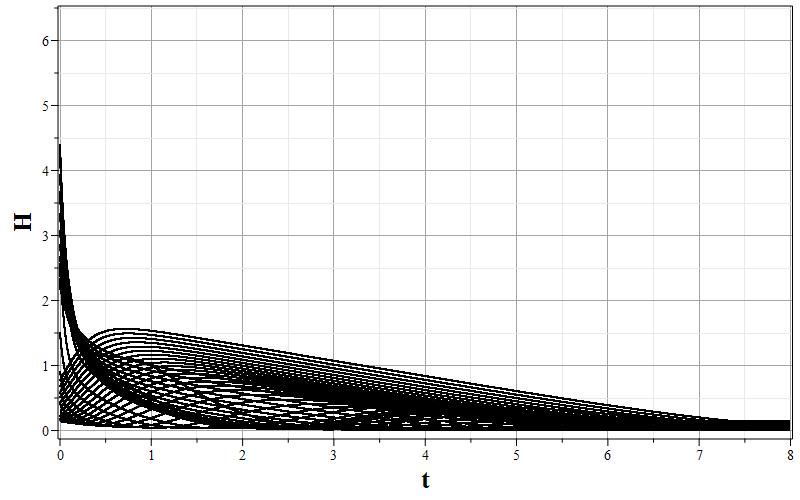
Рис. 1. Графики изменения параметров $\psi$, $z=\dot{\psi}$ и $h$ (соответственно, a,b,c) и фазовый портрет (d) $z=z(\psi)$ системы для $\xi=0.01$.

a	b
c	d

Рис. 2. Графики изменения параметров $\psi$, $z=\dot{\psi}$ и $h$ (соответственно, a,b,c) и фазовый портрет (d) $z=z(\psi)$ системы для $\xi=1.0$.

a	b
c	d

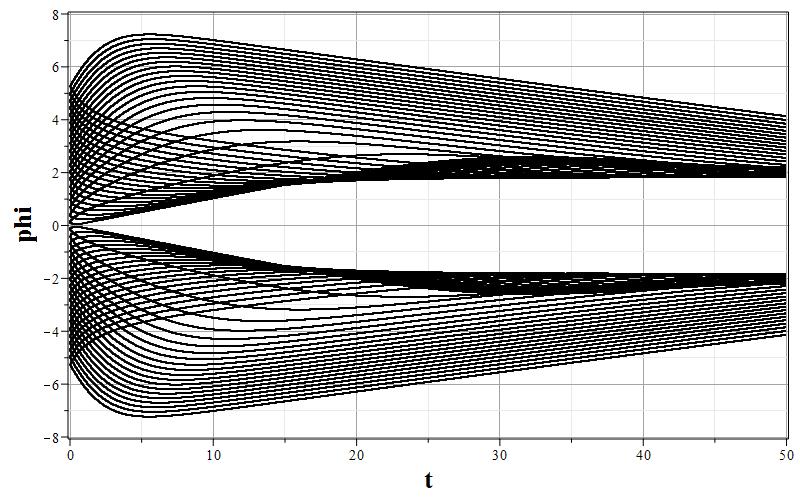
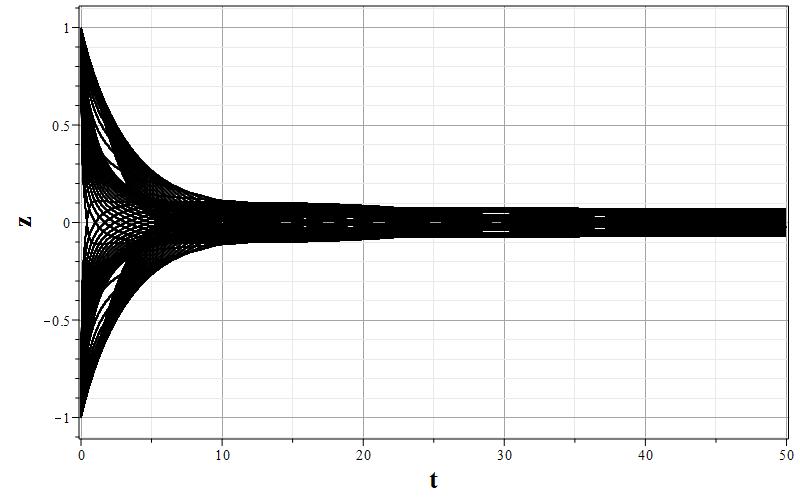
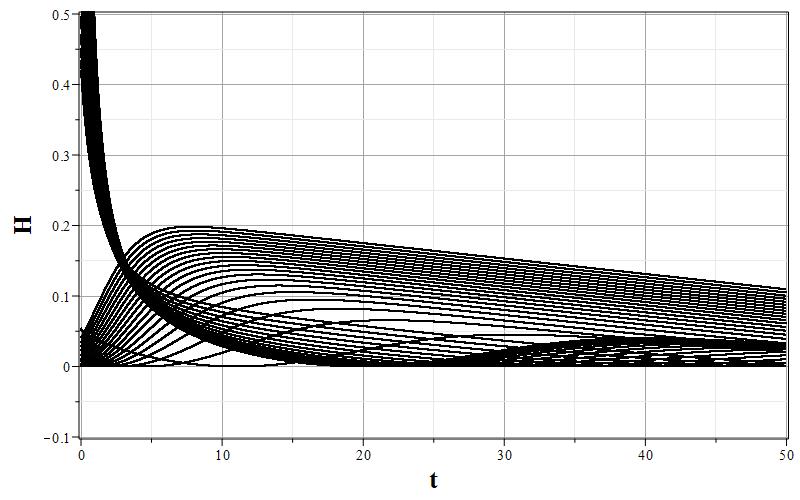
Рис. 3. Графики изменения параметров $\psi$, $z=\dot{\psi}$ и $h$ (соответственно, a,b,c) и фазовый портрет (d) $z=z(\psi)$ системы для $\xi=100.0$.

     Общая характеристика фазовых портретов соответствует расположению особых точек одинаковому для всех значений $\xi$. Характерным изменением при увеличении $\xi$ является ``сжатие'' графика фазового портрета по оси $z=\dot{\psi}$ так, что при очень больших $\xi$ все фазовые траектории очень быстро приближаются к оси абсцисс, а затем медленно приближаются к особым точкам. Это можно заметить, сравнивая масштаб фазовых портретов при $\xi=0.01$ и $\xi=100.0$. Отсюда можно сделать вывод, что при больших $\xi$ скалярное поле меняется очень медленно, но осциллирует с затуханием осцилляций при приближении к особым точкам $\psi_0=\pm w$.  При этом параметр Хаббла стремится к нулю, что соответствует степенной инфляции или фридмановской динамике. Начальный же этап эволюции с быстрым изменением поля соответствует экспоненциальной инфляции. Это хорошо видно на графиках зависимости $h=h(\tau)$ при всех значениях $\xi$. При малых значениях $\tau$ на всех графиках изменения масштабного фактора имеется область, где $h$ достигает максимума, или мало меняется.  Поскольку при больших $\xi$ малым параметром является величина $\varepsilon=\xi^{-1}$, то анализ динамики можно провести с помощью разложений по этому параметру.

Список литературы

%\bibitem{BezSha2007}
[1] F.~Bezrukov, M.~Shaposhnikov, arXiv:0710.3755

%\bibitem{DeFelice2011}
[2] A.~De Felice et al, arXiv:1105.4685

%\bibitem{Chervon:2019sey}
[3] S.~Chervon, I.~Fomin, V.~Yurov, and A.~Yurov, {\it Scalar Field Cosmology} (World Scientific, 2019).

%\bibitem{Kaiser1994}
[4] D.I. Kaiser, arXiv:astro-ph/9408044.

%\bibitem{ChZh2000iv}
[5] S.V. Chervon, V.M. Zhuravlev, Russ.Phys.J. 43 (2000) 11-17, Izv.Vuz.Fiz. 43N1 (2000) 14-20

%\bibitem{ZhCh2000jetf}
[6] V.M. Zhuravlev, S.V. Chervon, J.Exp.Theor.Phys. 91 (2000) 2, 227-238, Zh.Eksp.Teor.Fiz. 118 (2000) 2, 259-272